ВЫПУКЛАЯ ПОВЕРХНОСТЬ — область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… … Математическая энциклопедия
РИМАНОВО ПРОСТРАНСТВО ОБОБЩЕННОЕ — пространство с внутренней метрикой, подчиненное нек рым ограничениям на кривизну. К ним относятся пространства с кривизной, ограниченной сверху , и др. (см. [3]). Р. п. о. отличаются от римановых пространств не только большей общностью, но и тем … Математическая энциклопедия
ПОГРУЖЕННЫХ МНОГООБРАЗИЙ ГЕОМЕТРИЯ — теория, изучающая внешнюю геометрию и связь между внешней и внутренней . геометрией подмногообразий евклидова или риманова пространства. П. м. г. является обобщением классич. дифференциальной геометрии поверхностей в евклидовом пространстве .… … Математическая энциклопедия
ИЗОМЕТРИЧЕСКОЕ ПОГРУЖЕНИЕ — погружение k мерного метрич. многообразия М к в n мерное риманово пространство V, в виде k мерной поверхности Ф, при к ром расстояние между любыми двумя точками на М k совпадает с расстоянием между их образами, измеренным по поверхности Ф в… … Математическая энциклопедия
ВЫПУКЛОЕ МНОЖЕСТВО — в евклидовом или другом векторном пространстве множество, к рое вместе с любыми двумя точками содержит все точки соединяющего их отрезка. Пересечение любой совокупности В. м. есть В. м. Наименьшая размерность плоскости, содержащей данное В. м.,… … Математическая энциклопедия
Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр … Википедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
ВНУТРЕННЯЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий те свойства поверхности и фигур на ней, к рые зависят лишь от длин кривых, лежащих на поверхности, и тем самым могут быть определены без обращения к объемлющему пространству. К В. г. регулярных поверхностей относятся… … Математическая энциклопедия
ПСЕВДОВЫПУКЛОСТЬ И ПСЕВДОВОГНУТОСТЬ — свойства областей в комплексных пространствах, а также комплексных пространств и функций на них, аналогичные свойствам выпуклости и вогнутости областей и функций в пространстве . Вещественная функция j класса С 2 на открытом множестве наз. р… … Математическая энциклопедия
ДВУМЕРНОЕ МНОГООБРАЗИЕ ОГРАНИЧЕННОЙ КРИВИЗНЫ — метрическое пространство, являющееся двумерным многообразием с внутренней метрикой, для к рого определены аналоги таких понятий двумерной римановой геометрии, как длина и интегральная кривизна кривой, площадь и интегральная гауссова кривизна… … Математическая энциклопедия
, Xи Y - точки на них, х, у - расстояние от Одо X, Y, z - расстояние между 
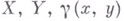- угол в плоском треугольнике со сторонами, равными х, у, z, лежащий против стороны, равной z. Условие выпуклости метрики (в точке О).состоит в том, что 
является невозрастающей функцией (т. е. 
при 
) на всякой паре промежутков 
такой, что точки Xи Y, соответствующие любым двум значением из этих промежутков, можно соединить кратчайшей. Внутренняя метрика является В. м. тогда и только тогда, когда она есть метрика неотрицательной кривизны. Метрика выпуклой поверхности является В. м. Обратно, любое двумерное многообразие с В. м. реализуется в виде выпуклой поверхности (теорема А. Д. Александрова).