ПСЕВДОВЫПУКЛОСТЬ И ПСЕВДОВОГНУТОСТЬ

свойства областей в комплексных пространствах, а также комплексных пространств и функций на них, аналогичные свойствам выпуклости и вогнутости областей и функций в пространстве 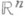. Вещественная функция j класса С ² на открытом множестве наз. р-псевдовыпуклой (или р- выпуклой), если эрмитова форма

имеет в каждой точке области Uне менее чем п=р+1 неотрицательных собственных значений. В случае, когда Н(j) имеет не менее чем n=р+1 положительных собственных значений, говорят, что j сильно (или строго) р- псевдовыпукла. В частности, (сильно) 1-псевдовыпуклые функции - это (строго) плюрисубгармонические функции класса С ². Функция на аналитич. множестве 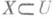наз. (сильно) р-выпуклой, если она является ограничением сильно р-псевдовыпуклой функции на U. Наконец, (сильно) р-выпуклая функция на произвольном комплексном пространстве X - это непрерывная функция на X, к-рая в окрестности любой точки представляется (сильно) р-выпуклой функцией в соответствующей локальной модели (см. Аналитическое пространство).

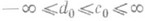Комплексное пространство Xназ. ( р, q )-выпукло - вогнутым, если существуют непрерывная функция и такие d₀, c₀, где , что для любых и 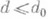множество

относительно компактно в X, а j сильно р-выпукла на и сильно (q-выпукла на 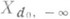. Если или , то пространство Xназ. сильно р-псевдовыпуклым или сильно q- вогнутым соответственно. Если же , то Xназ. р-полным.

Примеры. 1) Открытое множество Xс гладкой границей дХ в комплексном многообразии Мназ. строго р-псевдовыпуклым (строгор-псевдовогнутым), если всякая точка обладает окрестностью U, в к-рой существует такая сильно р-выпуклая функция j, что 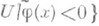(соответственно ) Всякое строго р-псевдовыпуклое (строго р-псевдовогнутое) относительно компактное открытое множество является сильно р-выпуклым (сильно р-вогнутым) многообразием. Если нен-рые компоненты границы дХ удовлетворяют условию р-псевдовыпуклости, а другие - условию q-псевдовогнутости, то получаются примеры ( р, q )-выпукло-вогнутых многообразий.

2) Компактные комплексные пространства естественно считать 0-выпуклыми.

3) Класс 1-полных пространств совпадает склассом Штейна пространств.

4) Класс сильно 1-выпуклых пространств совпадает с классом пространств, получающихся из пространств Штейна путем собственной модификации в конечном множестве точек.

5) Пусть X - компактное комплексное многообразие размерности n, S - его замкнутое подмногообразие, все компоненты к-рого имеют размерность q. Тогда XS является сильно (q+1 )-вогнутым, а если нормальное расслоение над Sположительно - сильно ( п-q )-выпуклым пространством.

6) Если S- замкнутое подмногообразие коразмерности рв многообразии Штейна X, то ХS р-полно.

7) Голоморфное векторное расслоение Еранга rнад многообразием Xназ. р-положительным (q-oтрицательным), если на Есуществует такая послойная эрмитова метрика h, что функция c(v)=-h(v, v).на Еявляется сильно ( р + r )-въшуклой (соответственно -cявляется сильно q-выпуклой) вне нулевого сечения (в случаях p=1 и q=1 получают понятия положительного расслоения и отрицательного расслоения). Если Xкомпактно, то пространство р-положительного расслоения Еявляется сильно ( р+r )-вогнутым, а пространство q-отрицательного расслоения - сильно q-выпуклым. Пространство голоморфного векторного расслоения над р-полным пространством всегда р-полно.

Для ( р, q )-выпукло-вогнутых пространств доказаны теоремы о конечномерности и отделимости нёк-рых пространств когомологий со значениями в когерентных аналитич. чках (см. Конечности теоремы в теории аналитических пространств). Аналогичные теоремы конечности доказаны также и для сильно ( р, q )-выпукло-вогнутых отображений (см. [1], [2]). Пространство Xявляется сильно 1-выпуклым тогда и только тогда, когда для всех rи любого когерентного аналитич. чка Fна X. Если Xр-полно, то H^r(X, F)=0 для всех и любого когерентного аналитич. чка Fна X.

Группы гомологии р-выпуклых и р-полных пространств обладают следующими свойствами. Если Xесть re-мерное приведенное сильно р-выпуклое (р-полное) комплексное пространство, то (соответственно для 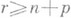. Для сильно 1-выпуклых пространств известно также, что группы 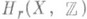конечно порождены при , а для р-полных многообразий, - что для и что группа свободна.

Комплексное пространство Xназ. псевдовогнутым, если в Xсуществует относительно компактное открытое множество U, пересекающее каждую неприводимую компоненту пространства Xи удовлетворяющее следующему условию: любая точка обладает такой окрестностью Vв X, что для любых точек , достаточно близких к х ₀,

для всех голоморфных функций f в V. Если Xесть n-мерное многообразие, , то достаточно, чтобы множество Uбыло сильно ( п-1)-псевдовогнутым в X. Любое компактное пространство псевдовогнуто. Для псевдовогнутых пространств Xдоказаны следующие теоремы конечности: пространство голоморфных сечений любого голоморфного векторного расслоения над X конечномерно; если X связно, то все голоморфные функции на Xпостоянны; поле мероморфных функций на Xесть поле алгебраич. функций, степень трансцендентности k-рого не превосходит dim X. Последняя теорема имеет важные приложения к автоморфным функциям, основанные на том, что пространство D/Г, где Г - собственно разрывная группа автоморфизмов ограниченной области Dв 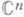, во многих случаях оказывается псевдовогнутым (в этом случае говорят, что Г - псевдовогнутая группа). Напр., псевдовогнутыми являются арифметич. подгруппы групп автоморфизмов ограниченных симметрич. областей.

Лит.: [1] Еrmine J. L., "Ann. Sc. norm. sup. Pisa. Cl. sci", 1979, v. 6, № 1, p. 1 -18; [2] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 15, М., 1977, с. 93-171.

А. Л. Онищик.