Теорема Больцано — Вейерштрасса — Теорема Больцано Вейерштрасса, или лемма Больцано Вейерштрасса о предельной точке предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства можно выделить сходящуюся… … Википедия
Эллиптические функции Вейерштрасса — Эллиптические функции Вейерштрасса одни из самых простых эллиптических функций. Этот класс функций (зависящих от эллиптической кривой) назван в честь Карла Вейерштрасса. Также их называют функциями Вейерштрасса, и используют для их… … Википедия
Теорема Вейерштрасса о функции на компакте — Теорема Вейерштрасса в математическом анализе и общей топологии гласит, что функция, непрерывная на компакте, ограничена на нём и достигает своей верхней и нижней грани. Содержание 1 Формулировка 2 Доказательство … Википедия
Теорема Вейерштрасса о функции, непрерывной на компакте — Теорема Вейерштрасса в математическом анализе и общей топологии гласит, что функция, непрерывная на компактe, ограничена на нём и достигает своей верхней и нижней грани. Содержание 1 Формулировка 2 Доказательство для R 3 Замечания … Википедия
Существенно особая точка — Изолированная особая точка функции , голоморфной в некоторой проколотой окрестности этой точки, называется существенно особой, если предел не существует. Содержание 1 … Википедия
Существенно особая точка — аналитической функции, точка z0 комплексной плоскости, в которой не существует ни конечного, ни бесконечного предела при z → z0 для функции, однозначной и аналитической в некоторой окрестности этой точки (см. Аналитические функции).… … Большая советская энциклопедия
Теорема Вейерштрасса об ограниченной возрастающей последовательности — утверждает, что любая ограниченная возрастающая последовательность имеет предел, причем этот предел равен ее точной верхней грани. Несмотря на простоту доказательства, эта теорема оказывается очень удобной для нахождения пределов многих… … Википедия
Теорема Сохоцкого — Вейерштрасса — теорема комплексного анализа, описывающая поведение голоморфной функции в окрестности существенной особой точки. Формулировка Теорема. Если точка z0 является существенно особой для функции f(z), аналитической в некоторой проколотой окрестности … Википедия
Теорема Вейерштрасса о целых функциях — У этого термина существуют и другие значения, см. Теорема Вейерштрасса. Теорема Любая целая функция , имеющая не более чем счётное количество нулей , где точка 0 нуль порядка , может быть представлена в виде бесконечного произведения вида … Википедия
Сохоцкого - Вейерштрасса теорема — теорема теории аналитических функций (См. Аналитические функции); всякая однозначная аналитическая функция в каждой окрестности существенно особой точки (См. Существенно особая точка) принимает значения, сколь угодно близкие к любому… … Большая советская энциклопедия
В. т. всегда существуют. Для римановых поверхностей эти результаты были получены К. Вейерштрассом (К. Weierstrass). Для алгебраич. кривых рода 
всегда существует не менее 
В. т., причем точно 
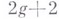их имеется только для гиперэллиптич. кривых. Верхняя граница для числа В. т. равна 
. Наличие В. т. на алгебраич. кривой Xрода 
гарантирует существование морфизма степени не выше 
кривой Xна прямую 
.