ЭНЕРГИЯ МЕР

- понятие потенциала теории, являющееся аналогом физич. понятия потенциальной энергии системы электрич. зарядов. Пусть для точек x=(x₁, . . ., x_n) евклидова пространства

- фундаментальное решение уравнения Лапласа и

- ньютонов (при или логарифмический (при п=2)потенциал борелевской меры на
Ограничиваясь пока случаем определяют взаимную энергию неотрицательных мер m и v равенством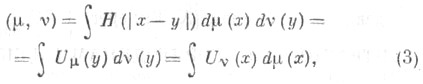

причем но может оказаться Энергия мер ы - это число 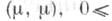Для мер 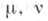произвольного знака можно воспользоваться канонич. разложениями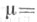 (или любыми разложениями вида и определить взаимную Э. м. равенством

причем взаимная Э. м. может оказаться и отрицательной, но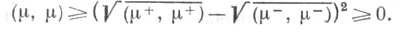

Совокупность всех мер с конечной энергией превращается в предгильбертово векторное пространство со скалярным произведением и энергетической нормой При этом выполняются 1) неравенство Буняковского и 2) принцип энергии: если 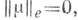то А. Картан (Н. Cartan) показал, что пространство 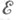не является полным, но множество неотрицательных мер полно в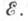
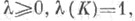Пусть K - компакт в Среди всех вероятностных мер на К, т. е. таких, что существует экстремальная емкостная мера с минимальной Э. м. к-рая связана с емкостью С(К)компакта Ксоотношением

Если потенциал меры допускает градиент с суммируемым квадратом, то имеет место равенство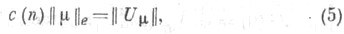

где

- нормаДирихле, а На самом деле равенство (5) остается в силе для любой меры 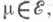причем норма Дирихле определяется при помощи соответствующего предельного перехода.
В случае плоскости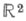 непосредственное применение для определения Э. м. формулы (3) с логарифмич. потенциалом (2) невозможно вследствие особого поведения логарифмич. ядра (1) на бесконечности. Пусть 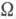- ограниченная область пространства 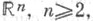допускающая функцию Грина g(x, у), и 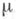- борелевская мера на Применяя в (3) вместо потенциалов U_v(x)потенциалы Грина вида

получают при определение Э. м., равносильное данному выше для мер на 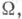к-рое, однако, оказывается пригодным и при п=2 с сохранением всех описанных свойств (причем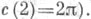

Лит.:[1] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964; [2] Уэрмер Дж., Теория потенциала, пер. с англ., М., 1980; [3] Ландкоф Н. С., Основы современной теории потенциала, М., 1966.
К. Д. Соломенцев.