- ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ
матрицы F(х) над кольцом многочленов k[x] - степени унитарных неприводимых многочленов над полем k, на к-рые разлагаются инвариантные множители матрицы F(x). Две
-матрицы над k[x],имеющие один и тот же ранг, тогда и только тогда эквивалентны (т. е. получаются одна из другой с помощью элементарных операций), когда они обладают одной и той же системой Э. д.
Элементарными делителями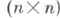
-матрицы . над полем kназ. Э. д. ее характеристич. матрицы || хE п -А||. Они могут быть получены следующим образом. Пусть Dl(x) - наибольший общий делитель миноров порядка l матрицы хЕ п -А, 
и D0=1. Тогда инвариантными множителями матрицы || хЕ n -А|| служат 
Множители il (х), отличные от 1, содержатся в
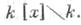Каждый из них представим в виде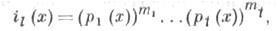 
где р i(x) - унитарные неприводимые над k многочлены,
Все полученные таким способом многочлены вида (р(х)) т и составят систему Э. д. матрицы А. Две квадратные матрицы над полем подобны тогда и только тогда, когда они имеют одну и ту же систему Э. д. Произведение всех Э. д. матрицы над полем совпадает с ее характеристич. многочленом, а наименьшее общее кратное ее Э. д. равно ее минимальному многочлену. Любой набор многочленов вида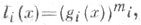 
где gi(x) - унитарный неприводимый над kмногочлен, служит системой Э. д. для одного и только одного класса подобных матриц над kпорядка n, где п - степень произведения многочленов li (х). Если k - поле разложения характеристич. многочлена матрицы А, то Э. д. матрицы Аимеют вид 
В этом случае число Э. д. равно числу клеток Жордана жордановой формы матрицы А, а Э. д.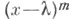 
соответствует жорданова клетка 
порядка . (см. Жорданова матрица). Квадратная матрица над полем . подобна диагональной матрице над kтогда и только тогда, когда каждый ее Э. д. имеет вид 
где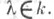 
Д. А. Супруненко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
