ЦЕЛАЯ ФУНКЦИЯ

- функция, аналитическая но всей плоскости комплексного переменного (кроме, возможно, бесконечно удаленной точки). Она разлагается в степенной ряд

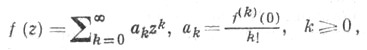
сходящийся во всей плоскости

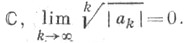
Если всюду, то f(z)=e^P(z), где Р(z)- Ц. <ф. Если имеется конечное число точек, в к-рых f(z) обращается в нуль, и эти точки - z₁, z₂, ..., z_k (их наз. нулями функции), то

где P(z) есть Ц. ф.
В общем случае, когда у f(z) имеется бесконечно много нулей z₁, z₂, . . ., имеет место представление (см. Вейерштрасса теорема о бесконечном произведении)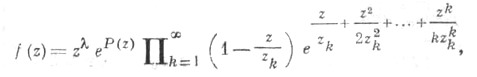

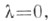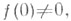где Р(z)есть Ц. ф., а если и равно кратности нуля z=0, если f(0)=0. Пусть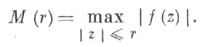

Если при больших r величина М(r) растет не быстрее то f(z) - многочлен степени не большей 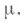Следовательно, если f(z) не многочлен, то М(r)растет быстрее любой степени r. При оценке роста М(r)в этом случае берется в качестве функции сравнения показательная функция.
По определению, f(z) есть Ц. ф. конечного порядка, если имеется конечное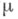 такое, что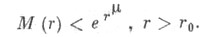

Нижняя грань 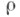множества чисел m, удовлетворяющих этому условию, наз. порядком Ц. ф. f(z). Порядок вычисляется по формуле

Если f(z) порядка 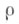удовлетворяет условию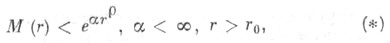

то говорят, что f(z) - функция порядка и конечного типа. Нижняя грань 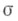множества чисел 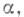удовлетворяющих указанному условию, наз. типом Ц. ф. f(z). Он определяется из формулы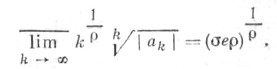

Среди Ц. ф. конечного типа различают Ц. ф. нормалъного типа 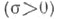и минимального типа 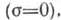Если условие (*) не выполняется при любом 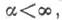то Ц. ф. наз. Ц. ф. максимального, или бесконечного, типа. Ц. ф. порядка 1 и конечного типа, а также Ц. ф. порядка ниже 1, характеризуемые условием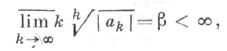

наз. Ц. ф. экспоненциального типа.
Нули z₁, z₂, . . . Ц. ф. f(z) порядка r обладают свойством:

Пусть р- наименьшее целое такое, что Тогда (см. Адамара теорема о целых функциях) имеет место представление

где Р(z) - многочлен степени не выше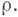
Для характеристики роста Ц. ф. f(z) конечного порядка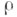 и конечного типа 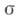вдоль лучей вводится величина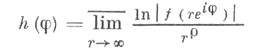

- роста индикатриса. Всегда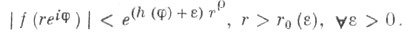

Если

где Е ₀ -в нек-ром смысле малое множество (множество нулевой относительной меры), то нули f(z) расположены на плоскости в определенном смысле весьма правильно и имеется точно описываемая связь между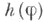 и характеристикой (плотностью) нулей. Функции f(z) с таким свойством наз. функциями вполне регулярного роста.
Функция многих переменных f(z₁, z₂, . . ., z_n )есть Ц. ф., если она является аналитической при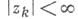 (k=1, 2, . . ., n). Для нее вводятся понятия порядка и типа (сопряженных порядков и типов). Простого представления в виде бесконечного произведения здесь получить не удается, потому что в отличие от случая п=1 нули f(z) не являются изолированными.

Лит.:[1] Евграфов М. А., Асимптотические оценки и целые функции, 3 изд., М., 1979; [2] Левин Б. Я., Распределение корней целых функций, М., 1956; [3] Ронкин Л. И., Введение в теорию целых функций многих переменных, М., 1971.
А. Ф. Леонтъев.