- ФРОБЕНИУСА АВТОМОРФИЗМ
элементгруппы Галуа специального вида, играющий фундаментальную роль в теории нолей классов. Пусть L - алгебраич. расширение конечного поля К. Тогда Ф. а. наз. автоморфизм
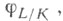 определяемый формулой
определяемый формулой 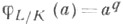 для всех
для всех  где
где 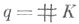 (мощность К). Если L/К-конечное расширение, то
(мощность К). Если L/К-конечное расширение, то 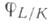 порождает группу Галуа G(L/K). Для бесконечного расширения L/K автоморфизм
порождает группу Галуа G(L/K). Для бесконечного расширения L/K автоморфизм 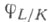 является топологич. образующей группы G(L/K). Если
является топологич. образующей группы G(L/K). Если  и
и 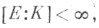 то
то 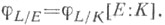
Пусть k - локальное поле с конечным полем вычетов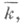 а К- неразветвленное расширение поля k.
а К- неразветвленное расширение поля k.
Тогда Ф. а.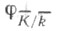 расширений полей вычетов однозначно продолжается до автоморфизма
расширений полей вычетов однозначно продолжается до автоморфизма 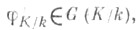 наз. Ф. а. неразветвлунного расширения K/k. Пусть
наз. Ф. а. неразветвлунного расширения K/k. Пусть 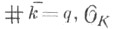 -кольцо целых элементов поля К и
-кольцо целых элементов поля К и 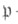 -максимальный идеал в
-максимальный идеал в 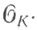 Тогда Ф. а.
Тогда Ф. а.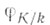 однозначно определяется условием
однозначно определяется условием 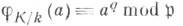 для любого
для любого 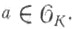 Если K/k- произвольное расширение Галуа локальных полей, то Ф. а. расширения K/k иногда называют любой автоморфизм
Если K/k- произвольное расширение Галуа локальных полей, то Ф. а. расширения K/k иногда называют любой автоморфизм 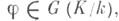 индуцирующий на максимальном неразветвленном подрасширении поля А Ф. а. в указанном выше смысле. Пусть K/k - расширение Галуа глобальных полей,
индуцирующий на максимальном неразветвленном подрасширении поля А Ф. а. в указанном выше смысле. Пусть K/k - расширение Галуа глобальных полей, 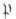 - простой идеал поля kи
- простой идеал поля kи 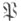 - нек-рый простой идеал поля К, лежащий над
- нек-рый простой идеал поля К, лежащий над 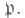 И пусть
И пусть 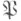 но разветвлен в расширении K/k и
но разветвлен в расширении K/k и 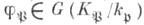 - Ф. а. неразветвленного расширения локальных полей
- Ф. а. неразветвленного расширения локальных полей 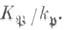 Отождествляя группу Галуа
Отождествляя группу Галуа 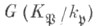 с подгруппой разложения идеала
с подгруппой разложения идеала 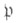 н G(K/k), можно рассматривать
н G(K/k), можно рассматривать 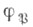 как элемент группы G(K/k). Этот элемент наз. Ф. а., соответствующим простому идеалу
как элемент группы G(K/k). Этот элемент наз. Ф. а., соответствующим простому идеалу 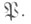 Если K/k - конечное расширение, то согласно теореме Чеботарева о плотности для любого автоморфизма
Если K/k - конечное расширение, то согласно теореме Чеботарева о плотности для любого автоморфизма 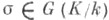 существует бесконечное число простых идеалов
существует бесконечное число простых идеалов 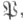 не разветвленных в K/k таких, что
не разветвленных в K/k таких, что 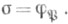 Для абелева расширения K/k элемент
Для абелева расширения K/k элемент 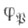 зависит только от
зависит только от 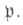 В этом случае
В этом случае  обозначается через
обозначается через 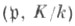 и наз. символом Артина простого идеала
и наз. символом Артина простого идеала 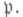
Лит.:[1] Вейль А., Основы теории чисел, пер. с англ., М., 1972.
Л. В. Кузьмин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
