УРЫСОНА УРАВНЕНИЕ

- нелинейное интегральное уравнение вида

где 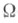- ограниченное замкнутое множество конечномерного евклидова пространства, К[ х,s, t], f(x)- заданные функции при Пусть функция К[ х, s, f] непрерывна по совокупности переменных - нек-рое положительное число) и пусть

Тогда, если

то уравнение

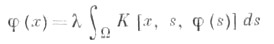
имеет единственное непрерывное решение удовлетворяющее неравенству Если 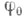- произвольная непрерывная функция, удовлетворяющая неравенству то последовательные приближения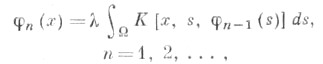

равномерно на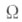 сходятся к
Пусть оператор Урысона

действует в пространстве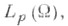 р> 1, для всех t₁, t₂, 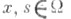выполняется неравенство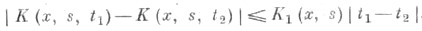

где K₁ - измеримая функция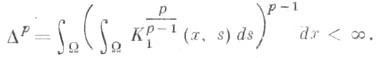

Тогда, при и 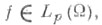уравнение (*) имеет в 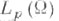единственное решение.
Уравнение (*) при определенных предположениях впервые было изучено П. С. Урысоном (см. Нелинейное интегральное уравнение).

Лит.:[1] Красносельский М. А., Топологические методы в теории нелинейных интегральных уравнений, М., 1956; [2] Интегральные уравнения, М., 1968 (Справочная матем. б-ка).
Б. В. Хведелидзе.