НЕЛИНЕЙНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

- интегральное уравнение, содержащее неизвестную функцию нелинейно. Ниже приведены основные классы Н. и. у., к-рые часто встречаются при исследовании различных прикладных задач и теория к-рых в определенной постановке достаточно хорошо разработана. Важным примером Н. и. у. является Урысона уравнение

где - замкнутое ограниченное множество конечномерного евклидова пространства,- заданная функция, наз. ядром, определенная при 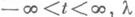- числовой параметр, - искомая функция.

П. С. Урысон (см. [2]) при определенных предположениях дал полное исследование спектра собственных значений уравнения (1), допускающих положительные собственные функции. Было показано, что положительные собственные функции 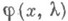соответствуют значениям 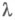только из нек-рого интервала причем является монотонно возрастающей функцие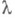й и

Частным случаем уравнения Урысона является Гаммерштейна уравнение:

где - известные функции. Теоремы существования и единственности впервые были установлены А. Гаммерштейном (см. [9]). Он исследовал уравнение (2) в предположении, что действительная функция 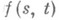непрерывна по совокупности аргументов и что самосопряженный в линейный интегральный оператор, порожденный ядром К, является положительным и действует вполне непрерывно из в пространство непрерывных функций.

Другим примером Н. и. у. является Ляпунова- Шмидта уравнение:

в к-рых функции и - заданные,- искомая, число iфиксировано, и суммирование распространено на всевозможные векторы с неотрицательными целочисленными компонентами. Левая часть равенства (3) наз. интегро-степенным рядом от двух функциональных аргументов ,

Уравнение типа (3) впервые рассмотрел А. М. Ляпунов (см. [1]), а позднее, в более общем виде, Э. Шмидт (см. [8]). В их исследованиях были заложены основы теории ветвления Н. и. у., целью к-рой является решение следующей задачи. Пусть ищется решение нелинейной задачи, зависящее от некоторых параметров, причем для некоторых их значений решение может разветвляться. Возникают вопросы о нахождении самого решения и тех значений параметров, при которых оно разветвляется, о числе ветвей и о представлении каждой ветви как функции параметров (см. [6]).

Теория Н. и. у. является частью общей теории нелинейных операторных уравнений. Именно, интегральные уравнения рассматриваются как конкретные иллюстрации соответствующих операторных уравнений. Для этого требуется выяснение общих свойств (непрерывность, полная непрерывность и т. д.) конкретных интегральных операторов, входящих в уравнение (см. [3] - [7]).

Лит.:[1] Ляпунов А. М., "Записки Академии Наук", СПБ, 1906, с. 1-225; [2] Урысон П. С, "Матем. сб.", 1923, т. 31, с. 236-55; [3] Вайнберг М. М., Вариационные методы исследования нелинейных операторов, М., 1956; [4] Красносельский М. А., Топологические методы в теории нелинейных интегральных уравнений, М., 1956; [5] Красносельский М. А. [и др.], Интегральные операторы в пространствах суммируемых функций, М., 1966; [6] Вайнберг М. М., Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [7] Вайнберг М. М., Вариационный метод и метод монотонных операторов в теории нелинейных уравнений, М., 1972; [8] Schmidt E., "Math. Ann.", 1908 Bd 65, S. 370-99; [9] Hammerstein A., "Acta math.", 1930, v. 54, p. 117-76.

Б. В. Хведелидзе.