- УОЛША СИСТЕМА
функций {Wn(x)} на отрезке [0, 1] -функции
 и
и 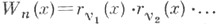
 при
при  где
где  k=0,1, 2, . . .,- функции Радемахера,
k=0,1, 2, . . .,- функции Радемахера, 
 v1>v2>...>vm>0 - двоичное представление числа
v1>v2>...>vm>0 - двоичное представление числа  Эта система была определена и исследована Дж. Уолтом [1], хотя еще в 1900 году Баррет использовал функции этой системы в вопросах связи при размещении проводников в открытых проводных линиях. В теории связи более предпочтительным является другое определение У. с. Именно, если
Эта система была определена и исследована Дж. Уолтом [1], хотя еще в 1900 году Баррет использовал функции этой системы в вопросах связи при размещении проводников в открытых проводных линиях. В теории связи более предпочтительным является другое определение У. с. Именно, если 
то функции Wn(x)определяются следующими рекуррентными формулами:

Системы {Wn(x)} и {W*n(x)} отличаются только нумерацией в пачках
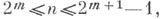 т=1, 2,. . . Например:
т=1, 2,. . . Например: 
 и т. д. Номер kфункции
и т. д. Номер kфункции  соответствует числу перемен знака этой функции в промежутке (0,1), т. е. является аналогом удвоенной частоты для синусоидальных функций. У. с. ортонормирована на отрезке [0,1] и ее можно рассматривать как естественное пополнение системы Радемахера.
соответствует числу перемен знака этой функции в промежутке (0,1), т. е. является аналогом удвоенной частоты для синусоидальных функций. У. с. ортонормирована на отрезке [0,1] и ее можно рассматривать как естественное пополнение системы Радемахера.
У. с. образуют коммутативную мультипликативную группу, единичным элементом в к-рой является функция W0(x). а обратным к Wk(x)является снова Wk(x).Лит.:[1] Walsh J. Z., лAmer. J. Math.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
