ТРАНСЦЕНДЕНТНОЕ РАСШИРЕНИЕ
- ТРАНСЦЕНДЕНТНОЕ РАСШИРЕНИЕ
расширение поля, не являющееся алгебраическим. Расширение К/k трансцендентно тогда и только тогда, когда поле Ксодержит элементы, трансцендентные над k, то есть элементы, не являющиеся корнем никакого алгебраич. уравнения с коэффициентами из k.
Элементы множества  наз. алгебраически независимыми над k, если для любого конечного набора
наз. алгебраически независимыми над k, если для любого конечного набора  и любого многочлена F(X1, . . ., Х т )с коэффициентами из k
и любого многочлена F(X1, . . ., Х т )с коэффициентами из k
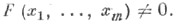
Элементы множества Xтрансцендентны над k. Если X- максимальное множество, все элементы к-рого алгебраически независимы над k, то Xназ. базисом трансцендентности поля Кнад k.
Мощность множества Xназ. степенью трансцендентности поля Кнад kи является инвариантом расширения K/k Для башни полей 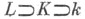 степень трансцендентности L/k равна сумме степеней трансцендентности L/K и K/k.
степень трансцендентности L/k равна сумме степеней трансцендентности L/K и K/k.
Если все элементы множества Xалгебраически независимы над k, то расширение k(X)наз. чисто трансцендентным. В этом случае поле k(X)изоморфно полю рациональных функций от множества переменных Xнад k. Любое расширение полей L/k представимо в виде башни расширений  где L/K - алгебраическое, a K/k - чисто трансцендентное расширение. Если поле Кможно выбрать так, чтобы L/K было сепарабельным расширением, то расширение L/k наз. сепарабельно порожденным, а базис трансцендентности Кнад k - сепарирующим базисом. Если . сепарабельно порождено над k, то Lсепарабельно над k. В случае когда расширение L/k конечно порождено, верно и обратное утверждение. Расширение K/k сепарабельно тогда и только тогда, когда любое дифференцирование поля kпродолжается на К. Такое продолжение определено однозначно для любого дифференцирования тогда и только тогда, когда расширение K/k алгебраично.
где L/K - алгебраическое, a K/k - чисто трансцендентное расширение. Если поле Кможно выбрать так, чтобы L/K было сепарабельным расширением, то расширение L/k наз. сепарабельно порожденным, а базис трансцендентности Кнад k - сепарирующим базисом. Если . сепарабельно порождено над k, то Lсепарабельно над k. В случае когда расширение L/k конечно порождено, верно и обратное утверждение. Расширение K/k сепарабельно тогда и только тогда, когда любое дифференцирование поля kпродолжается на К. Такое продолжение определено однозначно для любого дифференцирования тогда и только тогда, когда расширение K/k алгебраично.
Лит.:[1] Зарисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [2] Бурбаки Н., ' Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965.
Л. В. Кузьмин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ТРАНСЦЕНДЕНТНОЕ РАСШИРЕНИЕ" в других словарях:
РАСШИРЕНИЕ — п о л у г р у п п ы А полугруппа S, содержащая Ав качестве подполугруппы. Обычно речь идет о расширениях полугруппы А, связанных с Атеми или иными условиями. Наиболее развита теория идеальных Р. полугрупп (полугрупп, содержащих Ав качестве… … Математическая энциклопедия
Расширение поля — поле E, содержащее данное поле K в качестве подполя . Типы расширений Алгебраическое расширение расширение, все элементы которого являются алгебраическими над K, то есть любой элемент которого является корнем некоторого многочлена f(x) c… … Википедия
СЕПАРАБЕЛЬНОЕ РАСШИРЕНИЕ — п о л я расширение K/kтакое, что для нек рого натурального п поля Kи линейно разделены над k(см. Линейно разделенные расширения). Расширение, не являющееся сепарабельным, наз. н е с е п а р а б е л ь н ы м. В дальнейшем рассматриваются только… … Математическая энциклопедия
ДИСКРИМИНАНТ — 1) Д. многочлена f(x)=a0xn+a1 х n 1+...+ а n, с корни к рого равны a1, a2, ... , a п, произведение Д. равен нулю тогда и только тогда, когда многочлен имеет кратные корни. Д. симметричен относительно корней многочлена и поэтому может быть выражен … Математическая энциклопедия
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ — функция переменных x1,...xn удовлетворяющая уравнению где F неприводимый многочлен от с коэффициентами из нек рого поля K, наз. полем констант. А. ф., заданная над этим полем, наз. А. ф. над полем K. Многочлен часто записывается по степеням… … Математическая энциклопедия
Поле (алгебраич.) — Поле алгебраическое, важное алгебраическое понятие, часто используемое как в самой алгебре, так и в др. отделах математики и являющееся предметом самостоятельного изучения. Над обычными числами можно производить четыре арифметических действия… … Большая советская энциклопедия
Поле — I Поле 1) обширное, ровное, безлесное пространство. 2) В сельском хозяйстве участки пашни, на которые разделены площадь Севооборота, а также внесевооборотные (запольные) участки, используемые для выращивания с. х. растений. 3)… … Большая советская энциклопедия
НЁТЕР ПРОБЛЕМА — вопрос о рациональности поля инвариантов конечной группы, действующей автоморфизмами поля рациональных функций. Подробнее, пусть поле рациональных функций от п переменных с коэффициентами в поле рациональных чисел , т. е. К чисто трансцендентное… … Математическая энциклопедия
УНИРАЦИОНАЛЬНОЕ МНОГООБРАЗИЕ — алгебраическое многообразие Xнад полем k, для к рого существует такое рациональное отображение проективного пространства что плотно в Xи расширение полей рациональных функций k(Pn)/ k(X)сепарабельно. Другими словами, k(X)имеет сепарабельное чисто … Математическая энциклопедия
Дифференциальная теория Галуа — В этой статье отсутствует вступление. Пожалуйста, допишите вводную секцию, кратко раскрывающую тему статьи. Содержание … Википедия
 наз. алгебраически независимыми над k, если для любого конечного набора
наз. алгебраически независимыми над k, если для любого конечного набора  и любого многочлена F(X1, . . ., Х т )с коэффициентами из k
и любого многочлена F(X1, . . ., Х т )с коэффициентами из k 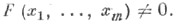
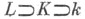 степень трансцендентности L/k равна сумме степеней трансцендентности L/K и K/k.
степень трансцендентности L/k равна сумме степеней трансцендентности L/K и K/k.  где L/K - алгебраическое, a K/k - чисто трансцендентное расширение. Если поле Кможно выбрать так, чтобы L/K было сепарабельным расширением, то расширение L/k наз. сепарабельно порожденным, а базис трансцендентности Кнад k - сепарирующим базисом. Если . сепарабельно порождено над k, то Lсепарабельно над k. В случае когда расширение L/k конечно порождено, верно и обратное утверждение. Расширение K/k сепарабельно тогда и только тогда, когда любое дифференцирование поля kпродолжается на К. Такое продолжение определено однозначно для любого дифференцирования тогда и только тогда, когда расширение K/k алгебраично.
где L/K - алгебраическое, a K/k - чисто трансцендентное расширение. Если поле Кможно выбрать так, чтобы L/K было сепарабельным расширением, то расширение L/k наз. сепарабельно порожденным, а базис трансцендентности Кнад k - сепарирующим базисом. Если . сепарабельно порождено над k, то Lсепарабельно над k. В случае когда расширение L/k конечно порождено, верно и обратное утверждение. Расширение K/k сепарабельно тогда и только тогда, когда любое дифференцирование поля kпродолжается на К. Такое продолжение определено однозначно для любого дифференцирования тогда и только тогда, когда расширение K/k алгебраично. 