- ДИСКРИМИНАНТ
- 1) Д. многочлена f(x)=a0xn+a1 х n-1+...+ а n, с
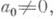 корни к-рого равны a1, a2, ... , a п,- произведение
корни к-рого равны a1, a2, ... , a п,- произведение
Д. равен нулю тогда и только тогда, когда многочлен имеет кратные корни. Д. симметричен относительно корней многочлена и поэтому может быть выражен через его коэффициенты.
Д. квадратного трехчлена ax2+bx+c равен b2-4ас;Д. многочлена x3+px+q (корни к-рого вычисляются по Кардано формуле )равен -27q2-4р 3. Если f(х) - многочлен над полем характеристики 0, то
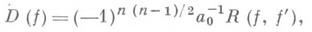
где R(f,f') - результант многочлена f(x)и его производной f'(x). Производной многочлена f(x) = a0xn +a1xn-1+...+an с коэффициентами из любого поля наз. многочлен па 0 х п-1+ (п-1) а 1 х n-2+...+ an-1.
Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975.
И. В. Проскуряков.
2) Д. <полуторалинейной формы f в базисе (u)= {u1, ... , un} - элемент из кольца А, равный
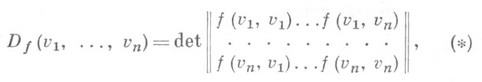
где (v)- фиксированный базис конечномерного свободного А-модуля Енад коммутативным кольцом Ас единицей, снабженным автоморфизмом а. Если (w)={w1, ... , wn} - другой базис в Е, а

- матрица перехода от (v)к (w), то
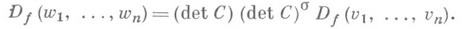
Если кольцо Ане имеет делителей нуля, то для невырожденности f необходимо и достаточно, чтобы

Если u1, ...,un- произвольный набор пэлементов из Е, то элемент Df(u1,... , un )кольца А , определяемый формулой (*), наз. дискриминантом f относительно системы u1, ...,un. Пусть Абез делителей нуля и f - невырожденная полуторалинейная форма. Тогда для того, чтобы система элементов u1, ..., un из Ебыла свободной, необходимо и достаточно, чтобы
 При этом u1,... , un будет базисом в Етогда и только тогда, когда Df(u1,... , un )и Df(u1, ..., и n )ассоциированны в Адля некоторого базиса u1, . . . , и п в А.
При этом u1,... , un будет базисом в Етогда и только тогда, когда Df(u1,... , un )и Df(u1, ..., и n )ассоциированны в Адля некоторого базиса u1, . . . , и п в А.Лит.:[1] Бурбаки Н.. Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [2] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974.
В. Л. Попов.
3) Д. системы элементов поля - одна из важных конструкций в теории расширений полей. Пусть К- конечное расширение поля kстепени п. Отображение
 в k:
в k: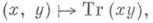
где х,
 a Tr a - след элементаявляется
a Tr a - след элементаявляется 
симметрической билинейной формой на поле K, рассматриваемом как линейное пространство над k. Д. этой билинейной формы (см. Дискриминант полуторалинейной формы) относительно системы элементов w1... ,wm из Кназ. дискриминантом системы w1, ...,wm и обозначается D(w1, ... ,wm). В частности, если указанная система есть базис Кнад к, то ее Д. наз. дискриминантом базиса K над k. Д. двух базисов отличаются множителем, являющимся квадратом нек-рого ненулевого элемента поля k. Д. всякого базиса Кнад кне равен нулю тогда и только тогда, когда расширение К/k сепарабельно. Если fx(t)- многочлен степени га, являющийся минимальным многочленом элемента хиз сепарабельного расширения К/к, то D(1, х, х 2,..., х т )совпадает с Д. многочлена fx(t). Приведенные определения могут быть перенесены также на случай произвольной конечномерной ассоциативной алгебры над полем (см. ниже п. 4).
В случае сепарабельного расширения К/k Д. базиса w1, .. . , wn может быть вычислен по формуле

где s1, .. ., sn - все различные вложения Кв фиксированное алгебраич. замыкание поля к, оставляющие неподвижным k.
Пусть k=Q- поле рациональных чисел, К- поле алгебраич. чисел и М- некоторый модуль ранга пв К. Тогда для любых двух базисов модуля Мзначения Д. совпадают и это общее значение Д. наз. дискриминантом модуля М. Если Мсовпадает с кольцом целых чисел поля К, то Д. модуля Мназ. просто дискриминантом поля К и обозначается Dk. Число Dk, является важной характеристикой поля К. Напр., если Кдопускает s вещественных и 2t комплексных вложений в поле комплексных чисел С, то

где zk(q)- дзета-функция Дедекинда, h- число классов дивизоров, R- регулятор поля К и т- число корней из единицы в поле К. Имеется оценка

которая показывает, что
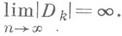 Для квадратичного поля
Для квадратичного поля 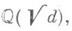 где d- свободное от квадратов целое рациональное число,
где d- свободное от квадратов целое рациональное число, 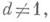 имеют место формулы:
имеют место формулы: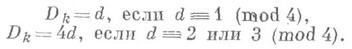
Для кругового поля K=Q(s), где е - примитивный корень р r -й степени
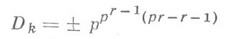 из единицы (знак минус берется при р r=4 или p=3(mod 4), а плюс - в остальных случаях).
из единицы (знак минус берется при р r=4 или p=3(mod 4), а плюс - в остальных случаях).Указанное определение Д. модуля в поле алгебраич. чисел может быть обобщено на тот случай, когда к- поле частных дедекиндова кольца А, a К- конечное еепарабельное расширение поля кстепени п. Пусть В- целое замыкание кольца Ав Ки b - произвольный дробный идеал кольца В. Тогда дискриминантом идеала b наз. А-модуль D(6), порожденный всеми Д. вида D(w1, ... , wn), где {w1, ... , wn} пробегает всевозможные базисы поля Кнад к, лежащие в b. D(b) оказывается дробным идеалом кольца А, причем имеет место равенство D(b) = N(b)2D (В), где N(b) - норма идеала b. Д. D(В)совпадает с нормой дифференты кольца Внад А.
Лит.:[1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Ленг С, Алгебраические числа, пер. с англ., М., 1966; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [4] Джекобсон Н., Теория колец, пер. с англ., М., 1947.
В. Л. Попов.
4) Д. алгебры - Д. симметричной билинейной формы ( х, у)=Т( ху), где х, у- элементы конечномерной ассоциативной алгебры Анад полем F, а Т(а)- главный след элемента
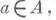 определяемый следующим образом. Пусть e1, . . ., е n- к.-л. базис алгебры A, Ф = F(x1, ..., xn) - чисто трансцендентное расширение поля Fс помощью алгебраически независимых элементов x1, ... ,xn,
определяемый следующим образом. Пусть e1, . . ., е n- к.-л. базис алгебры A, Ф = F(x1, ..., xn) - чисто трансцендентное расширение поля Fс помощью алгебраически независимых элементов x1, ... ,xn, 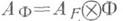 - соответствующее скалярное расширение алгебры А, тогда элемент x=x1e1+....+xn е n ОA Ф наз. общим элементом алгебры А, а минимальный многочлен (над Ф) элемента х- минимальным многочленом алгебры А. Пусть
- соответствующее скалярное расширение алгебры А, тогда элемент x=x1e1+....+xn е n ОA Ф наз. общим элементом алгебры А, а минимальный многочлен (над Ф) элемента х- минимальным многочленом алгебры А. Пусть
- минимальный многочлен алгебры А; коэффициенты mi(x). оказываются на самом деле многочленами из F[x1, ... , xn]. Если
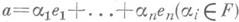 - произвольный элемент из A, то т 1(a1, ... , an)= Т(а)наз. главным следом элемента a, mr(a1, . .. ,a п)=N (а)- главной нормой, а многочлен g(t;a1 , ... ,an).- главным многочленом. Коэффициенты главного многочлена для данного элемента
- произвольный элемент из A, то т 1(a1, ... , an)= Т(а)наз. главным следом элемента a, mr(a1, . .. ,a п)=N (а)- главной нормой, а многочлен g(t;a1 , ... ,an).- главным многочленом. Коэффициенты главного многочлена для данного элемента  не зависят от выбора базиса, поэтому упомянутая выше билинейная форма ( х, у )на Аопределена инвариантно, в то время как ее Д. определен с точностью до мультипликативного множителя, являющегося квадратом ненулевого элемента из F. Алгебра Асепарабельна (см. Сепарабельная алгебра )тогда и только тогда, когда ее Д. отличен от нуля.
не зависят от выбора базиса, поэтому упомянутая выше билинейная форма ( х, у )на Аопределена инвариантно, в то время как ее Д. определен с точностью до мультипликативного множителя, являющегося квадратом ненулевого элемента из F. Алгебра Асепарабельна (см. Сепарабельная алгебра )тогда и только тогда, когда ее Д. отличен от нуля.Лит.:[1] Джекобсон Н., Теория колец, пер. с англ., М., 1947.
Е. Н. Кузьмин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
