ТРАНЗИТИВНАЯ ГРУППА

ТРАНЗИТИВНАЯ ГРУППА

- группа подстановок (G, X )такая, что каждый элемент может быть переведен в любой элемент подходящим элементом 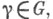т. е. 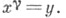Иными словами, все множество Xобразует единственную орбиту группы (G, X). Если же число орбит больше 1, то группа (G, X)наз. интранзитивной. Орбиты интранзитивной группы иногда наз. ее областями транзитивности. У интранзитивной группы (G, X) с орбитами Xi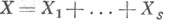


ограничение действия группы на X;транзитивно. Пусть Н - подгруппа в Gи пусть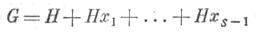


- разложение Gна правые смежные классы по Н. Пусть, далее, Х={ Нх i}. Тогда действие (G, X )определяется условием Это действие транзитивно, и обратно, всякое транзитивное действие подобно вышеуказанному для подходящей подгруппы H в G.
Действие (G, X)наз. . раз транзитивным, если для любых двух упорядоченных множеств из kразличных элементов (х 1, . . ., х k )и (у 1, . . ., yk), 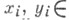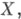существует такой элемент 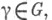что 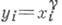для всех i=l, . . ., k;иначе говоря, (G, X)обладает лишь одной антирефлексивной k-орбитой. Для k-транзитивная группа наз. кратнотранзитивной. Примером дважды транзитивных групп являются группы целых линейных преобразований 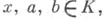нек-рого поля К. Примером трижды транзитивных групп служат группы дробно-линейных преобразований проективной прямой над полем К, т. е. преобразований вида


где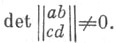

Т. г. (G, X)наз. строго k раз транзитивной, если лишь тождественная подстановка может оставлять на месте kразличных элементов из 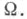Группа целых линейных и группа дробно-линейных преобразований являются примерами строго дважды и строго трижды транзитивных групп.
Конечная симметрич. группа Sn n раз транзитивна. Конечная знакопеременная группа А п ( п-2) раза транзитивна. Эти две серии кратно транзитивных групп считаются тривиальными. Известны еще две 4 раза транзитивные группы М 11 и М 23 и две 5 раз транзитивные группы M12 и М 24 (см. [3], а также Матьё группа). Существует гипотеза (1984), что за исключением этих четырех групп не существует нетривиальных kраз транзитивных групп для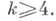 Эта гипотеза доказана в предположении, что верна неоднократно анонсированная классификация конечных простых неабелевых групп [6]. Более того, при указанном предположении можно считать законченной классификацию всех кратно транзитивных групп.
Т. г. определяются также для дробных . вида т+1/2, m=0, 1, 2, .... А именно, группа (G, X) наз. 1/2- транзитивной, если либо |Х|=1, либо все орбиты группы (G, X)имеют одинаковую длину большую 1. А для п>1 группа (G, X) п+1/2 раз транзитивна, если фиксатор (Gx, X) п-1/2 раз транзитивен на X(см. [3]).

Лит.:[1] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969; [2] Холл М., Теория групп, пер. с англ., М., 1962; [3] Wiе1andt Н., Finite permutation groups, N. Y.- L., 1964; [4] Passman D., Permutation groups, N. Y.- Amst., 1968; [5] Higman D. G., Lecture on permutation representation, Giessen, 1977; [6] Cameron P. J., лBull. London Math. Soc.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "ТРАНЗИТИВНАЯ ГРУППА" в других словарях:

  • ПРИМИТИВНАЯ ГРУППА ПОДСТАНОВОК — группа подстановок (G; M), сохраняющая лишь тривиальные отношения эквивалентности на множестве М(т. е. равенство и аморфную эквивалентность). Изучаются главным образом конечные П. г. п. П. г. п. транзитивна и всякая 2 транзитивная группа… …   Математическая энциклопедия

  • ИМПРИМИТИВНАЯ ГРУППА — группа Gвзаимно однозначных отображений на себя ( подстановок )нек рого множества S, для к рой существует разбиение множества Sв объединение непересекающихся подмножеств S1, . . ., Sm, обладающее следующими свойствами: число элементов хотя бы в… …   Математическая энциклопедия

  • КОНЕЧНАЯ ГРУППА — группа с конечным числом элементов. Это число наз. порядком группы. Исторически К. г. послужили исходным материалом для формирования многих понятий абстрактной теории групп. Обычно говорят, что целью теории К. г. является описание, с точностью до …   Математическая энциклопедия

  • ПОДСТАНОВОК ГРУППА — совокупность подстановок на нек ром множестве X, образующих группу относительно операции умножения подстановок. Иначе, П. г. это пара (G, X), где G группа, X множество и каждому соответствует подстановка множества Xтакая, что 1) , , и 2) х a=х… …   Математическая энциклопедия

  • ЦАССЕНХАУЗА ГРУППА — дважды транзитивная группа Gподстановок конечного множества М, в к рой лишь единичная подстановка оставляет на месте более двух символов из М, и для любой нары символов подгруппа Н а,b нетривиальна, где впервые такие группы рассмотрены X.… …   Математическая энциклопедия

  • ДВИЖЕНИЙ ГРУППА — непрерывная группа преобразований пространства, элементами к рой являются движения этого пространства, а групповой операцией последовательное выполнение в указанном порядке двух движений. В широком смысле, любая группа непрерывных преобразований… …   Математическая энциклопедия

  • ФЛАГОВАЯ СТРУКТУРА — 1) то же, что флаг. 2) Ф. с. типа v=(n1, п 2, .... п k )на n мерном многообразии М дифференциально геометрич. структура, к рая представляет собой поле флагов Fx типа v, определяемых подпространствами V1(x),V2(x) ..., Vk(x) в касательных… …   Математическая энциклопедия

  • ПСЕВДОГРУППА — преобразований дифференцируемого многообразия М семейство диффеоморфизмов открытых подмножеств многообразия Мв М, замкнутое относительно композиции отображений, перехода к обратному отображению, а также сужения и склейки отображений. Точнее,… …   Математическая энциклопедия

  • ПСЕВДОГРУППОВАЯ СТРУКТУРА — на многообразии M максимальный атлас Агладких локальных диффеоморфизмов многообразия Мна фиксированное многообразие V, все функции перехода между к рыми принадлежат данной псевдогруппе Г локальных преобразований многообразия V. Псевдогруппа Г наз …   Математическая энциклопедия

  • АРИСТОТЕЛЬ — (ок. 384 322 до н.э.), древнегреческий философ и педагог, родился в Стагире в 384 или 383 до н.э., умер в Халкиде в 322 до н.э. Почти двадцать лет Аристотель учился в Академии Платона и, по видимому, какое то время там преподавал. Покинув… …   Энциклопедия Кольера


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»