БОРЕЛЕВСКОЕ МНОЖЕСТВО

БОРЕЛЕВСКОЕ МНОЖЕСТВО

B-множество,- множество, к-рое может быть получено в результате не более чем счетной совокупности операций объединения и пересечения открытых и замкнутых множеств топологич. пространства. Более точно, борелевским множеством наз. элемент наименьшего замкнутого относительно дополнений счетно аддитивного класса множеств, содержащего замкнутые множества. Другие названия Б. м.: множества, измеримые по Борелю, В - измерим. <ые множества. Открытые и замкнутые множества наз. Б. м. нулевого порядка. Б. м. первого порядка наз. множества типа 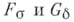, являющиеся, соответственно, счетными суммами замкнутых и счетными пересечениями открытых множеств. Б. м. второго порядка наз. множества типа 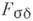(пересечение счетного числа множеств типа 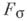) н множества типа 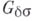(сумма счетного числа множеств типа ). Так, по индукции, определяются р. м. любого конечного порядка. Эта классификация может быть продолжена при помощи трансфинитных чисел второго класса, и ею исчерпываются все Б. м. Если 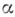- какое-нибудь трансфинитное число второго класса, то Б. м. класса наз. все Б. м. порядка 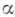, не являющиеся Б. м. порядка 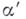ни при каком 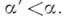Непустота классов Б. м. зависит от основного пространства, в к-ром ведется рассмотрение. В евклидовом, гильбертовом и бэровском пространствах существуют Б. м. любого класса.

Б. м. представляет собой частный случай А -множеств. Для того чтобы A- множество Ебыло Б. м., необходимо и достаточно, чтобы дополнение к Етакже было А-множеством (М. Я. Суслин). В пространствах, где введена Лебега мера, всякое Б. м. является измеримым по Лебегу. Обратное неверно. В любом сепарабельном пространстве мощности континуум существуют множества, не являющиеся Б. м.

Б. м. введены Э. Борелем [1]; они играют важную роль при изучении борелевских функций.

В более общем понимании Б. м. - множество любой борелевской системы множеств, порожденной нек-рой системой множеств. Б. м. топологич. пространства порождаются системой замкнутых подмножеств этого пространства.

Лит.:[1] Воrе1 Е., Legons sur les fonctions discontinues, P., 1898; [2] Куратовский К., Топология, т. 1, М., 1966; [3] Хаусдорф Ф., Теория множеств, пер. с нем., М.-Л., 1937; [4] Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948. В. А. Скворцов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "БОРЕЛЕВСКОЕ МНОЖЕСТВО" в других словарях:

  • ДВУСТОРОННЕЕ БОРЕЛЕВСКОЕ МНОЖЕСТВО — класса a борелевское подмножество метрического или (более широко) совершенно нормального топояогич. пространства, являющееся одновременно множеством аддитивного класса aи мультипликативного класса а, т. е. принадлежащее одновременно классам Fa и… …   Математическая энциклопедия

  • МНОЖЕСТВО ТИПА — множество ( множество), объединение (пересечение) счетного числа замкнутых (открытых) множеств. См. Борелевское множество. А МНОЖЕСТВО, аналитическое множество, в полном сепарабельном метрическом пространстве непрерывный образ борелевского… …   Математическая энциклопедия

  • Борелевское поле — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… …   Википедия

  • ЦИЛИНДРИЧЕСКОЕ МНОЖЕСТВО — множество S в векторном пространстве Lнад полем действительных чисел задаваемое уравнением где i =1,2, ... линейные функции, oпределенные на L, а борелевское множество в п мерном пространстве n= 1, 2, ... . Совокупность всех Ц. м. в Lобразует… …   Математическая энциклопедия

  • Множеств теория —         учение об общих свойствах множеств, преимущественно бесконечных. Понятие множества, или совокупности, принадлежит к числу простейших математических понятий; оно не определяется, но может быть пояснено при помощи примеров. Так, можно… …   Большая советская энциклопедия

  • МЕРА — множества, обобщение понятия длины отрезка, площади фигуры, объема тела, интуитивно соответствующее массе множества при нек ром распределении массы по пространству. Понятие М. множества возникло в теории функций действительного переменного в… …   Математическая энциклопедия

  • СУСЛИНА ТЕОРЕМА — (в дескриптивной теории множеств) 1) Существует А множество (числовой прямой не являющееся борелевским множеством. 2) Для того чтобы данное А множество было борелевским, необходимо и достаточно, чтобы его дополнение было также А множеством. 3)… …   Математическая энциклопедия

  • Борелевская сигма-алгебра — это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (также она содержит и все замкнутые). Эти подмножества также называются Борелевыми. Если не оговорено противное, в качестве топологического… …   Википедия

  • Борелева функция — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… …   Википедия

  • Борелевская функция — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»