- СТЕПЕНЬ ОТОБРАЖЕНИЯ
степень непрерывного отображения
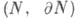связных компактных многообразий одинаковой размерности - целое число degf такое, что 
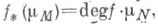где 
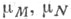- фундаментальные классы многообразий M и Nнад кольцом 
или 
- индуцированное отображение. В случае неориентированных многообразий С. о. однозначно определена по mod 2. Если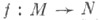 
- дифференцируемое отображение замкнутых дифференцируемых многообразий, то degf совпадает mod 2 с числом прообразов регулярного значения уотображения f. В случае ориентированных многообразий 
где sign Jx - знак якобиана отображения f в точке х(степень Брауэра),
Для непрерывного отображения
и изолированной точки хв прообразе нуля определено понятие локальной степени degx f в точке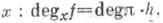 
где h - сужение отображения f на маленькую сферу 
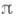- проекция из нуля на единичную сферу. В случае дифференцируемого f справедлива формула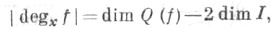 
где Q(f) - кольцо ростков гладких функций в нуле, профакторизованное по идеалу, порожденному компонентами f, I - идеал факторкольца, максимальный по отношению к свойству I2=Q. Пусть
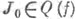- класс якобиана отображения f, тогда для линейного функционала 
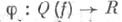такого, что 
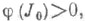выполнено 
где 
- симметричная билинейная форма на Q(f). Лит.:[1] Дольд А., Лекции по алгебраической топологии, пер. с англ., М., 1976; [2] Милнор Дж., Уоллес А., Дифференциальная топология, пер. с англ., М., 1972; [3] Арнольд В. И., Варченко А. Н., Гусейн-3аде С. М., Особенности дифференцируемых отображений, М., 1982; [4] Eisenbud D., Levine H., лAnn. Math.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
