- СПРЯМЛЯЕМАЯ КРИВАЯ
- кривая, имеющая конечную длину. Пусть Г - непрерывная параметрич. кривая в трехмерном евклидовом пространстве
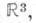т. е. Г={x1=x1(t), x2=x2(t), x3=x3(t)},
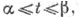~ где xk(t), k=l, 2, 3 - непрерывные на отрезке 
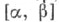функции,
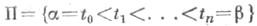- произвольное разбиение отрезка 
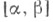и Aj(x1(tj), x2(tj), x3(tj)) - порожденная им последовательность точек на кривой Г. И пусть Г п - ломаная, вписанная в кривую Г и имеющая вершины в точках А 0, А1, . . ., А n. Длина этой ломаной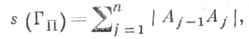 
где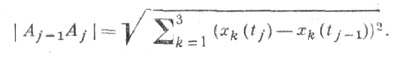
Величина
наз. длиной кривой Г. Длина s(Г) не зависит от способа параметризации кривой Г. Если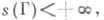 
то кривая Г наз. спрямляемой кривойи. С. к.
Г имеет касательную почти во всех своих точках A(x1(t),x2(t),x3(t)). т. е. почти при всех значениях параметра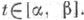
Изучение С. к. было начато Л. Шеффером [1] и продолжено К. Жорданом [2], к-рый доказал, что кривая Г спрямляема тогда и только тогда, когда все три функции xk(t), k=l, 2, 3, являются ограниченной вариации функциями на отрезке 
Лит.:[1] Sсheеffеr L., лActa math.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
