СПЕКТРАЛЬНАЯ ОЦЕНКА ПАРАМЕТРИЧЕСКАЯ

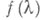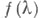- оценка спектральной плотности стационарного случайного процесса, отвечающая нек-рой фиксированной параметрич. модели (т. е. гипотезе о том, что функция принадлежит определенному семейству спектральных плотностей, описываемых конечным числом параметров). При нахождении С. о. п. данные наблюдений над процессом используются лишь для оценки неизвестных параметров модели, т. е. задача оценивания спектральной плотности здесь сводится к статистич. задаче оценки параметров. Наиболее широко используемой на практике С. о. п. является спектральная оценка максимальной энтропии, отвеча- ющая допущению, что функция представляет собой квадрат нек-рого тригонометрич. многочлена фиксированного порядка. Более общий класс С. о. п., сравнительно часто применяющийся в прикладных задачах, опирается на использование модели смешанного процесса авторегрессии-сколъзящего среднего, т. е. на предположение о том, что представляет собой отношение квадратов модулей двух тригонометрич. многочленов фиксированных порядков (см. [1]-[3]).

Лит.:[1] Nonlinear methods of spectral analysis, В.- [а. о.], 1979; [2] Kей С. М., Марпл С. Л., лТр. ин-та инж. электротехн. радиоэлектр.