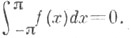СОПРЯЖЕННЫЙ КЛАСС ФУНКЦИИ
- СОПРЯЖЕННЫЙ КЛАСС ФУНКЦИИ
понятие теории функций, являющееся конкретным отображением двойственности в функциональных пространствах. Так, если класс функций Xрассматривается как банахово или топологическое векторное пространство, то С. к. ф. наз. класс функций, изометрически изоморфный сопряженному пространству X*. Напр., между пространствами  и
и 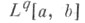 при
при 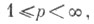
 существует изометрич. изоморфизм, при к-ром соответственные элементы х* и gсвязаны соотношением
существует изометрич. изоморфизм, при к-ром соответственные элементы х* и gсвязаны соотношением
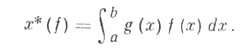
Если рассматривается нек-рый класс 2p-периодических суммируемых на 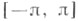 функций X, то С. к. ф. наз. класс функций, сопряженных к функциям из X. Напр., класс функций, сопряженных к
функций X, то С. к. ф. наз. класс функций, сопряженных к функциям из X. Напр., класс функций, сопряженных к 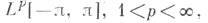 совпадает с классом таких функций f из
совпадает с классом таких функций f из  что
что

Класс функций, сопряженных к Lipa,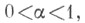 совпадает с классом таких функций из Lipa, что
совпадает с классом таких функций из Lipa, что
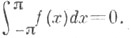
Лит.:[1] Freehet М., лС. r. Acad. sci.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "СОПРЯЖЕННЫЙ КЛАСС ФУНКЦИИ" в других словарях:
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… … Математическая энциклопедия
ИНДЕКСА ФОРМУЛЫ — соотношения между аналитич. и топологич. инвариантами операторов нек рого класса. Именно, И. ф. устанавливают связь между аналитич. индексом линейного оператора (L0, L1 топологич. векторные пространства), определяемым формулой и измеряющим таким… … Математическая энциклопедия
ПОЛУГРУППА ОПЕРАТОРОВ — семейство операторов {Т} вбанаховом или топологическом векторном пространстве, обладающее тем свойством, что композиция любых двух операторов семейства снова принадлежит семейству. Если операторы Т занумерованы элементами нек рой абстрактной… … Математическая энциклопедия
ПСЕВДОДИФФЕРЕНЦИАЛЬИЫЙ ОПЕРАТОР — оператор, действующий в функциональных пространствах на дифференцируемом многообразии и локально по определенным правилам записываемый с помощью нек poй функции, обычно наз. символом П. о., и удовлетворяющей оценкам производных определенного типа … Математическая энциклопедия
ЛИНЕЙНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — в узком смысле оператор, действующий на функции, заданные на открытом множестве и принимающий значения в поле или по формуле где функции со значениями в том же поле, наз. коэффициентами А. Если коэффициенты принимают значения во множестве матриц… … Математическая энциклопедия
ОПЕРАТОР — отображение одного множества на другое, каждое из к рых наделено нек рой структурой (алгебраич. операциями, топологией, отношением порядка). Общее определение О. совпадает с определением отображения или функции: пусть Xи Y два множества;… … Математическая энциклопедия
МАРКОВСКИЙ СТАЦИОНАРНЫЙ ПРОЦЕСС — марковский процесс, являющийся стационарным случайным процессом. М. с. п., отвечающий однородной марковской переходной функции, существует тогда и только тогда, когда существует стационарное начальное распределение m(А), отвечающее этой функции,… … Математическая энциклопедия
ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия
Торговля — (теория). Под Т. разумеют промысловую деятельность, имеющую целью преодолевать препятствия, разделяющие производителей и потребителей во времени и пространстве. Это определение (Ван дер Боргт) шире общепринятого, по которому Т. заключается в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Цехи в Западной Европе — Содержание: 1) Определение Ц. 2) Происхождение Ц. 3) Общая характеристика Ц. 4) Организация Ц. 5) Хозяйственная структура Ц. 6) Политическая роль Ц. 7) Эволюция средневековой цеховой организация. 8) Упадок Ц. 9) Литература. 1) Определение Ц.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
 и
и 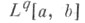 при
при 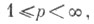
 существует изометрич. изоморфизм, при к-ром соответственные элементы х* и gсвязаны соотношением
существует изометрич. изоморфизм, при к-ром соответственные элементы х* и gсвязаны соотношением 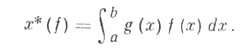
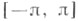 функций X, то С. к. ф. наз. класс функций, сопряженных к функциям из X. Напр., класс функций, сопряженных к
функций X, то С. к. ф. наз. класс функций, сопряженных к функциям из X. Напр., класс функций, сопряженных к 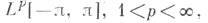 совпадает с классом таких функций f из
совпадает с классом таких функций f из  что
что 
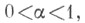 совпадает с классом таких функций из Lipa, что
совпадает с классом таких функций из Lipa, что