СОБОЛЕВА ОБОБЩЕННАЯ ПРОИЗВОДНАЯ

СОБОЛЕВА ОБОБЩЕННАЯ ПРОИЗВОДНАЯ

- локально суммируемая обобщенная производная от локально суммируемой функции (см. Обобщенная функция).
Подробнее, если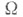 есть открытое множество в п- мерном пространстве 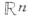и F(x)и f(x) - заданные на 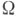локально суммируемые функции, то f(x)есть обобщенная частная производная по х j поСоболеву от функции F(x) на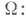


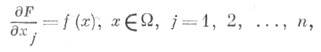
если выполняется равенство

для любых бесконечно дифференцируемых финитных в 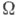функций 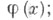эта производная - С. о. п.- определена только почти всюду на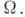
Другое эквивалентное определение С. о. п.: пусть локально суммируемую на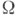 функцию F(x)можно видоизменить на множестве n-мерной меры нуль так, что она будет локально абсолютно непрерывной по х j для почти всех в смысле ( п-1)-мерной меры точек (х 1,...,xj-l. xj+l,..., х n). Тогда функция F будет иметь обычную частную производную xj почти для всех 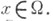Если она локально суммируема, то она и наз. С. о. п.
Третье эквивалентное определение С. о. п.: пусть для определенных на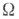 функций F(х)и f(х)можно подобрать последовательность непрерывно дифференцируемых на 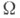функций {Fk(x)}таких, что для любой области 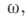замыкание к-рой принадлежит 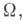имеет место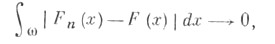


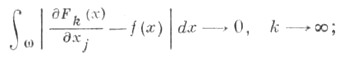
тогда f(x) есть С. о. п. от F(х) на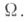
По индукции определяются С. о. п. на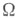 от F(если они существуют) более высокого порядка: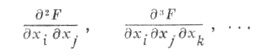

Они не зависят от порядка дифференцирования, напр.

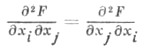
почти всюду на

Лит.:[1] Соболев С. Л., Некоторые применения функционального анализа в математической физике, [2 изд.], Новосиб., 1962; [2] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975.
С. М. Никольский.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "СОБОЛЕВА ОБОБЩЕННАЯ ПРОИЗВОДНАЯ" в других словарях:

  • СОБОЛЕВА ПРОСТРАНСТВО — пространство функций f=f(x)=f(x1,...,xn), определенных на множестве (обычно открытом) и интегрируемых с р йстепенью их модуля вместе со своими обобщенными производными до порядка lвключительно Норма функции определяется при помощи равенства Здесь …   Математическая энциклопедия

  • Пространство Соболева — (в математике)  функциональное пространство, состоящее из функций из пространства Лебега ( ), имеющих обобщенные производные заданного порядка из . При пространства Соболева являются банаховыми пространствами, а при p=2 пространства Соболева …   Википедия

  • ВЛОЖЕНИЯ ТЕОРЕМЫ — теоремы, относящиеся к циклу вопросов, посвященных изучению неравенств между нормами одной и той же функции, принадлежащей к разным классам (нормированным пространствам). Обычно речь идет о двух классах и , где есть часть и при этом выполняется… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — обобщение оператора дифференцирования. Д. о. (вообще говоря, не непрерывный, не ограниченный и не линейный) оператор, определенный нек рым дифференциальным выражением и действующий в пространствах (вообще говоря, векторнозначных) функций (или… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»