- СЕКВЕНЦИЙ ИСЧИСЛЕНИЕ
одна из формулировок предикатов исчисления. Благодаря удобной форме вывода С. и. находит широкое применение в доказательств теории, основаниях математики, при автоматич. поиске вывода. С. и. было предложено Г. Генценом в 1934 (см. [1]). Ниже приводится один из вариантов классич. исчисления предикатов в форме С. и.
Н а б о р о м ф о р м у л наз. конечное множество формул нек-рого логико-математического языка W, причем в этом множестве допускаются повторения формул. Порядок формул в наборе Г несуществен, но для каждой формулы указано, в скольких экземплярах она присутствует в Г. Набор формул может быть и пустым. Набор jГ получается из Г присоединением одного экземпляра формулы j. С е к в е н ц и е й наз. фигура вида
 , где Г и D - наборы формул, Г наз. а н т е ц е д е н т о м секвенции, а D-ее с у к ц е д е н т о м.
, где Г и D - наборы формул, Г наз. а н т е ц е д е н т о м секвенции, а D-ее с у к ц е д е н т о м.
Аксиомы С. и. имеют вид
 , где Г, D - произвольные наборы формул, а j - произвольная атомарная (элементарная) формула. Правила вывода исчисления устроены очень симметрично и вводят логич. связки в антецедент или сукцедент секвенции:
, где Г, D - произвольные наборы формул, а j - произвольная атомарная (элементарная) формула. Правила вывода исчисления устроены очень симметрично и вводят логич. связки в антецедент или сукцедент секвенции:
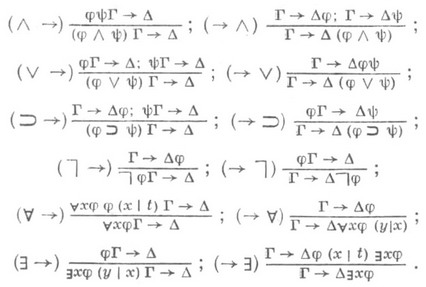
Здесь в правилах
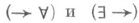 предполагается, что переменная уне есть параметр Г и D, а x не есть параметр j.
предполагается, что переменная уне есть параметр Г и D, а x не есть параметр j.
С. и. эквивалентно обычной форме исчисления предикатов в том смысле, что формула j выводима в исчислении предикатов тогда и только тогда, когда секвенция
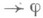 выводима в С. и. Для доказательства этого утверждения существенна основная теорема Генцена (или теорема о нормализации), к-рая для С. и. может быть сформулирована следующим образом: если в С. и. выводимы секвенции
выводима в С. и. Для доказательства этого утверждения существенна основная теорема Генцена (или теорема о нормализации), к-рая для С. и. может быть сформулирована следующим образом: если в С. и. выводимы секвенции 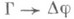 и
и 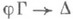 , то выводима и секвенция
, то выводима и секвенция 
Правило вывода
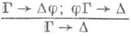 наз. правилом сечения, и теорема о нормализации утверждает, таким образом, что правило сечения допустимо в С. и. или что добавление правила сечения не изменяет объема выводимых секвенций. Ввиду этого теорему Генцена наз. также теоремой об устранении сечения.
наз. правилом сечения, и теорема о нормализации утверждает, таким образом, что правило сечения допустимо в С. и. или что добавление правила сечения не изменяет объема выводимых секвенций. Ввиду этого теорему Генцена наз. также теоремой об устранении сечения.
Симметричное устройство С. и. в значительной мере облегчает изучение его свойств, поэтому в теории доказательств важное место занимает поиск секвенциальных вариантов прикладных исчислений: арифметики, анализа, теории типов и доказательство для таких исчислений теоремы об устранении сечения в той или иной форме (см. [2], [3]). Найдены секвенциальные варианты и для многих исчислений, основанных на неклассич. логиках - интуиционистской, модальных и релевантных логиках и др. (см. [3], [4]).
Лит.:[1] Математическая теория логического вывода. Сб. переводов, М., 1967; [2] Т а к е у т и Г., Теория доказательств, пер. с англ., М., 1978; [3] Д р а г а л и н А. Г., Математический интуиционизм. Введение в теорию доказательств, М., 1979; [4] Ф е й с Р., Модальная логика, пер. [с англ.], М., 1974.
А. Г. Драгалин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
