- ПРЕДИКАТОВ ИСЧИСЛЕНИЕ
формальная аксиоматич. теория; исчисление, предназначенное для описания логических законов, справедливых для любой непустой области объектов с произвольными заданными на этих объектах предикатами (т. в. свойствами и отношениями).
Для формулировки П. и. следует вначале формулировать точный логико-математический язык W. В наиболее распространенном случае односортных языков 1-го порядка такой язык содержит предметные переменные х, у,z, . . ., функциональные символы f, g, h,... с различным количеством аргументных мест и предикатные символы (предикатные буквы) Р, Q, R,... также с различным количеством аргументных мест. Из переменных и функциональных символов конструируются термы языка, содержательно интерпретируемые как имена объектов исследования теории. Далее, если Ресть n-местный предикатный символ языка
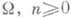 , a tl ,..., tn - термы, то Р(t1, . . ., tn).есть, по определению, атомарная (элементарная) формула языка W. Содержательно Р(t1, . . ., tn).означает, что истинно высказывание, гласящее, что объекты t1 ,..., tn связаны отношением Р.
, a tl ,..., tn - термы, то Р(t1, . . ., tn).есть, по определению, атомарная (элементарная) формула языка W. Содержательно Р(t1, . . ., tn).означает, что истинно высказывание, гласящее, что объекты t1 ,..., tn связаны отношением Р.
Из атомарных формул с помощью пропозициональных связок и кванторов конструируются формулы языка. Обычный набор связок и кванторов в классическом и интуиционистском П. и. таков: a или
 (конъюнкция, "и"),
(конъюнкция, "и"), 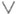 (дизъюнкция, неразделительное "или"),
(дизъюнкция, неразделительное "или"), 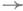 или
или  (импликация, "влечет", "если..., то"),
(импликация, "влечет", "если..., то"), 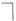 (отрицание, "не"),
(отрицание, "не"),  (квантор "для всех"), $ (квантор "существует"). Соответственно неэлементарные формулы этих исчислений имеют вид
(квантор "для всех"), $ (квантор "существует"). Соответственно неэлементарные формулы этих исчислений имеют вид 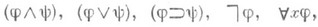 $xj. Вхождение переменной хв формулу j наз. связанным, если хвходит в часть j вида $xj или
$xj. Вхождение переменной хв формулу j наз. связанным, если хвходит в часть j вида $xj или 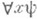 . Остальные вхождения хв j наз. свободными. Переменная хназ. параметром j, если найдется хотя бы одно свободное вхождение хв j. Интуитивно говоря, формула с параметрами выражает нек-рое условие, к-рое превращается в конкретное высказывание, если задать модель исчисления, т. е. выбрать нек-рую непустую область объектов исследования и приписать предикатным символам предикаты (т. е. отношения на области объектов), а параметрам приписать в качестве значений определенные объекты.
. Остальные вхождения хв j наз. свободными. Переменная хназ. параметром j, если найдется хотя бы одно свободное вхождение хв j. Интуитивно говоря, формула с параметрами выражает нек-рое условие, к-рое превращается в конкретное высказывание, если задать модель исчисления, т. е. выбрать нек-рую непустую область объектов исследования и приписать предикатным символам предикаты (т. е. отношения на области объектов), а параметрам приписать в качестве значений определенные объекты.
П. и. задается с помощью аксиом и правил вывода. Напр., одна из обычных формулировок классического исчисления предикатов содержит следующие аксиомы:
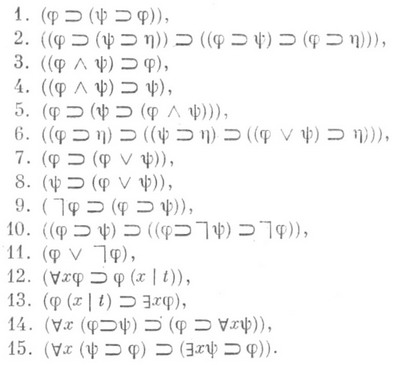
Здесь j, y, h обозначают произвольные формулы языка W, так что каждая из строчек 1-15 представляет собой аксиомную схему, порождающую конкретную аксиому исчисления при конкретном выборе формул j, y, h. Далее, в схемах 14 и 15 предполагается, что х - не параметр формулы ф; в схемах 12 и 13 через j(x|t). обозначен результат одновременного замещения всех свободных вхождений переменной хв ср на терм t(причем если tоказался на месте хв части формулы j, имеющей вид $yj или
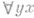 , где увходит в t, то следует дополнительно заменить все связанные вхождения ув эту часть на переменную, не входящую в j; это делается для того, чтобы не допустить искажения смысла j при замене хна t;такое искажение смысла наз. коллизией переменных).
, где увходит в t, то следует дополнительно заменить все связанные вхождения ув эту часть на переменную, не входящую в j; это делается для того, чтобы не допустить искажения смысла j при замене хна t;такое искажение смысла наз. коллизией переменных).
Далее, П. и. содержит два правила вывода: 1) если выведены формулы вида j и (
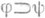 ), то разрешается вывести формулу y (правило модус поненс).и 2) если выведена формула j и х - переменная, то разрешается вывести формулу
), то разрешается вывести формулу y (правило модус поненс).и 2) если выведена формула j и х - переменная, то разрешается вывести формулу 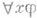 (правило обобщения).
(правило обобщения).
Истолкование логич. связок в П. и. такое же, как и в высказываний исчислении. Что касается истолкования кванторов, то они в классическом П. и. трактуются с использованием актуальной бесконечности. Если задать интерпретацию языка, то каждая формула без параметров получает значение "истина" или "ложь". Формула наз. классически общезначимой, если она в любой интерпретации и при любом приписывании значений параметрам принимает значение "истина". В силу Гёделя теоремы о полноте в классическом П. и. выводимы все классически общезначимые формулы и только они. Эта теорема представляет собой точное выражение идеи формализации классич. логики: в классическом П. и. выводятся все логич. законы, общие для всех моделей.
Интуиционистское исчисление предикатов отличается от классического тем, что из числа аксиомных схем исключается схема И. Различие двух исчислений отражает различное понимание логич. связок и кванторов. В последнем исчислении это понимание трактуется в рамках интуиционизма. Вопрос о полноте интуиционистского П. и. оказывается значительно сложнее и допускает различные решения в зависимости от деталей интуиционистской семантики, но и здесь может быть развита весьма содержательная теория моделей, аналогичная классич. моделей теории (см. Крипке модели, Реализуемость).
Употребляются и другие формулировки П. и., среди к-рых с точки зрения доказательств теории наиболее важны исчисления натурального вывода (см. Естественный логический вывод).и секвенций исчисление.
П. и. является обычным базисом для построения логич. исчислений, предназначенных для описания фрагментов тех или иных конкретных математич. теорий. Напр., если мы стремимся описать нек-рый класс истинных суждений теории множеств, то можно построить логич. исчисление в языке теории множеств, в к-ром, кроме аксиом и правил вывода классического П. и. (логич. постулатов), будут фигурировать дополнительные нелогические аксиомы, описывающие свойства множеств. Примером типичной нелогич. аксиомы в теории множеств является выбора аксиома.
П. и. иногда наз. узким исчислением предикатов, исчислением предикатов 1-го порядка, функциональным исчислением 1-го порядка, в отличие от исчислений, содержащих кванторы по предикатам и соответствующие аксиомы свертывания, утверждающие существование соответствующих предикатов. Такого рода исчисления, уже не носящие чисто логич. характера, часто наз. П. и. высшего порядка. Примером такого исчисления может служить типов теория. Помимо классического и интуиционистского П. и., имеются и другие логич. системы, описывающие логич. законы, к-рые могут быть выражены иными логич. средствами или с иных методологич. позиций. Сюда относятся П. и. модальной, индуктивной логики и др.
Лит.:[1] Гильберт Д., Бернайс П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., 2 изд., М., 1982; [2] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [3] Новиков П. С.,
Элементы математической логики, 2 изд., М., 1973; [4] Таксути Г., Теория доказательств, пер. с англ., М., 1978.
А. Г. Драгалин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
