БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ

БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ

коэффициенты при степенях z в разложений Ньютона бинома 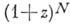. Б. к. обозначается 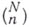или 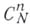и равен


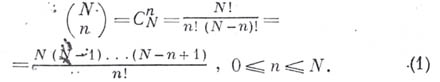
Обозначение 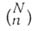восходит к Л. Эйлеру (L. Euler); второе обозначение 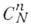появилось в 19 в. и связано, по-видимому, с интерпретацией Б. к. 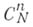как числа различимых неупорядоченных сочетаний из Nразличных объектов по пв каждом сочетании. Б. к. наиболее удобно выписываются в виде арифметического треугольника, или Паскаля треугольника, построение к-рого основано на свойстве Б. к.


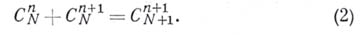
Как понятие Б. к., так и арифметич. треугольник в более или менее развитой форме были известны еще математикам древности, Б. Паскаль (В. Pascal) составил подробное исследование (1665) свойств Б. к. Кроме соотношения (2), имеется много других полезных соотношений между Б. к., напр.:


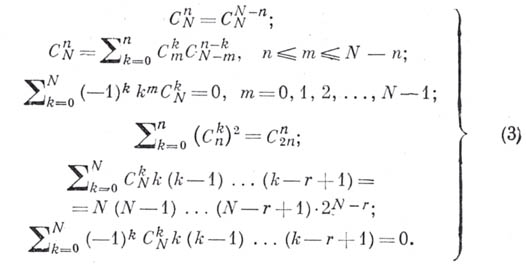
В частности, отсюда получается


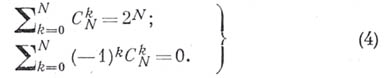
Использование Стирлинга формулы позволяет получать приближенные выражения для Б. к. Напр., если Nмного больше п:

На случай любого комплексного числа 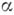Б. к. обобщаются по формуле


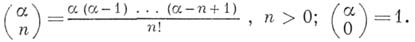
При этом нек-рые из соотношений (2) - (4) сохраняются, но, вообще говоря, в измененном виде. Напр.,


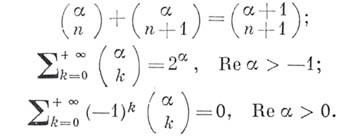
Таблицы Б. к. см. [2], [3].

Лит.:[1] Кори Г., Корн Т., Справочник по математике, пер. с англ., 2 изд., М., 1973; [2] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [3] Table of binomial coefficients, Cambridge, 1954. Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Полезное


Смотреть что такое "БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ" в других словарях:

  • Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы …   Википедия

  • Биномиальные коэффициенты —         коэффициенты в формуле разложения Ньютона бинома …   Большая советская энциклопедия

  • Биномиальные коэффициенты — так называются количества: l, n/1, n(n 1)/(1.2), n(n 1)(n 2)/(1.2.3)..., n(n 1)(n 2)...(n m + 1)/(1.2.3...m), составляющие коэффициенты последовательных членов бинома Ньютона (см. Бином). Их обозначают в настоящее время часто знаком . Общий вид Б …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

  • Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… …   Википедия

  • Биномиальный коэффициент — В математике биномиальные коэффициенты  это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В …   Википедия

  • Ньютона бином —         название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно:                  (1)          (1) где n целое положительное число, а и b какие угодно числа.… …   Большая советская энциклопедия

  • Бином Ньютона — Бином Ньютона  формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где   биномиальные коэффициенты,   неотрицательное целое число. В таком виде эта формула была известна… …   Википедия

  • биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… …   Энциклопедический словарь

  • Последовательность Падована — Последовательность Падована  это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 …   Википедия

  • Бином ньютона — Бином Ньютона  это формула , где   биномиальные коэффициенты, n  неотрицательное целое число. Содержание 1 Доказательство …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»