Биномиальные коэффициенты
- Биномиальные коэффициенты
-
так называются количества: l, n/1, n(n —1)/(1.2), n(n — 1)(n — 2)/(1.2.3)..., n(n — 1)(n — 2)...(n — m + 1)/(1.2.3...m), составляющие коэффициенты последовательных членов бинома Ньютона (см. Бином). Их обозначают в настоящее время часто знаком
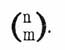
. Общий вид Б. коэффициента может быть написан кратко следующим образом:
где n! = 1.2.3…n и т. п. Б. коэффициенты обладают многими интересными свойствами, которые легко получаются как частные случаи свойств членов самого бинома Ньютона. Вот некоторые из этих свойств: ряд Б. коэффициентов имеет один максимум, для n больше 1, или один минимум, для n меньше 1. Сумма всех Б. коэффициентов равна 2n. С увеличением и до бесконечности ряд Б. коэффициентов стремится совпасть с рядом значений функции е–x². Если n есть число простое, то всякий Б. коэффициент делится на n и др.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон.
1890—1907.
Смотреть что такое "Биномиальные коэффициенты" в других словарях:
Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых чисел n и k. Явные формулы … Википедия
Биномиальные коэффициенты — коэффициенты в формуле разложения Ньютона бинома … Большая советская энциклопедия
БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ — коэффициенты при степенях z в разложений Ньютона бинома . Б. к. обозначается или и равен Обозначение восходит к Л. Эйлеру (L. Euler); второе обозначение появилось в 19 в. и связано, по видимому, с интерпретацией Б. к. как числа различимых… … Математическая энциклопедия
Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… … Википедия
Биномиальный коэффициент — В математике биномиальные коэффициенты это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В … Википедия
Ньютона бином — название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно: (1) (1) где n целое положительное число, а и b какие угодно числа.… … Большая советская энциклопедия
Бином Ньютона — Бином Ньютона формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где биномиальные коэффициенты, неотрицательное целое число. В таком виде эта формула была известна… … Википедия
биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… … Энциклопедический словарь
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия
Бином ньютона — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия
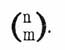 . Общий вид Б. коэффициента может быть написан кратко следующим образом:
. Общий вид Б. коэффициента может быть написан кратко следующим образом: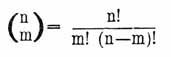 где n! = 1.2.3…n и т. п. Б. коэффициенты обладают многими интересными свойствами, которые легко получаются как частные случаи свойств членов самого бинома Ньютона. Вот некоторые из этих свойств: ряд Б. коэффициентов имеет один максимум, для n больше 1, или один минимум, для n меньше 1. Сумма всех Б. коэффициентов равна 2n. С увеличением и до бесконечности ряд Б. коэффициентов стремится совпасть с рядом значений функции е–x². Если n есть число простое, то всякий Б. коэффициент делится на n и др.
где n! = 1.2.3…n и т. п. Б. коэффициенты обладают многими интересными свойствами, которые легко получаются как частные случаи свойств членов самого бинома Ньютона. Вот некоторые из этих свойств: ряд Б. коэффициентов имеет один максимум, для n больше 1, или один минимум, для n меньше 1. Сумма всех Б. коэффициентов равна 2n. С увеличением и до бесконечности ряд Б. коэффициентов стремится совпасть с рядом значений функции е–x². Если n есть число простое, то всякий Б. коэффициент делится на n и др.