РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
- РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
-линейное однородное обыкновенное дифференциальное уравнение 2-го порядка в комплексной плоскости, имеющее три заданные регулярные особые точки а, b, с с соответствующими характеристич. показателями a. a', b, b', g, g' в этих точках. Общий вид такого уравнения впервые выписал Э. Паппериц (Е. Papperitz), из-за чего оно также наз. Папперица уравнением. Решения Р. д. у. записываются в виде так наз. Р- фу н к ц и и Р и м а н а
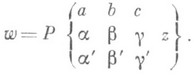
Р. д. у. принадлежит Фукса классу уравнений с тремя особыми точками. Частным случаем Р. д. у. является гипергеометрическое уравнение (особые точки:  ); поэтому само Р. д. у. иногда наз. о б о б щ е н н ы м г и п е р г е о м е т р и ч е с к и м у р а в н е н и е м. Р. д. у. приводится к Похгаммера уравнению, а потому решение Р. д. у. можно записать в виде интеграла по специальному контуру в комплексной плоскости.
); поэтому само Р. д. у. иногда наз. о б о б щ е н н ы м г и п е р г е о м е т р и ч е с к и м у р а в н е н и е м. Р. д. у. приводится к Похгаммера уравнению, а потому решение Р. д. у. можно записать в виде интеграла по специальному контуру в комплексной плоскости.
Лит. см. при ст. Папперица уравнение. Н. X. Розов.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "РИМАНА ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ" в других словарях:
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… … Математическая энциклопедия
Дифференциальное уравнение в частных производных — (частные случаи также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные. Содержание 1 Введение 2 История … Википедия
Дифференциальное уравнение с частными производными — Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные… … Википедия
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБЫКНОВЕННОЕ — уравнение, в к ром неизвестной является функция от одного независимого переменного, причем в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков. Термин дифференциальные уравнения был предложен Г.… … Математическая энциклопедия
Дифференциальное уравнение Римана — Дифференциальное уравнение Римана обобщение гипергеометрического уравнения, позволяющее получить регулярные сингулярные точки (англ.)русск. в любой точке сферы Римана. Названо в честь математика Бернхарда Римана. Содержание … Википедия
Уравнение в частных производных — Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ) дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные… … Википедия
Уравнение Лапласа — Уравнение Лапласа дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так: и является частным случаем уравнения Гельмгольца. Уравнение рассматривают также в двумерном и одномерном… … Википедия
ФУКСА УРАВНЕНИЕ — уравнение класса Фукса линейное однородное обыкновенное дифференциальное уравнение в комплексной области с аналитич. оэффициентами, все особые точки к рого на Римана сфере являются регулярными особыми точками. Для того чтобы уравнение (1)… … Математическая энциклопедия
ЛИНЕЙНОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ И СИСТЕМА — дифференциальное уравнение (и система) с частными производными вида у к poro в любой точке х=( х 0, x1 . . ., х n).области его задания среди действительных переменных y0, y1 . . ., yn можно выделить (в случае надобности после надлежащего… … Математическая энциклопедия
ТЕЛЕГРАФНОЕ УРАВНЕНИЕ — дифференциальное уравнение с частными производными Этому уравнению удовлетворяет напряжение тока в проводе, рассматриваемое как функция времени tи расстояния sот нек рой фиксированной точки провода. Здесь с скорость света, емкостный, индуктивный… … Математическая энциклопедия
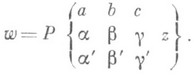
 ); поэтому само Р. д. у. иногда наз. о б о б щ е н н ы м г и п е р г е о м е т р и ч е с к и м у р а в н е н и е м. Р. д. у. приводится к Похгаммера уравнению, а потому решение Р. д. у. можно записать в виде интеграла по специальному контуру в комплексной плоскости.
); поэтому само Р. д. у. иногда наз. о б о б щ е н н ы м г и п е р г е о м е т р и ч е с к и м у р а в н е н и е м. Р. д. у. приводится к Похгаммера уравнению, а потому решение Р. д. у. можно записать в виде интеграла по специальному контуру в комплексной плоскости.