регулярное представление — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN regular representation … Справочник технического переводчика
Регулярное выражение — Регулярные выражения (англ. regular expressions, сокр. RegExp, RegEx, жарг. регэкспы или регексы) система синтаксического разбора текстовых фрагментов по формализованному шаблону, основанная на системе записи образцов для поиска. Образец (англ.… … Википедия
ИНДУЦИРОВАННОЕ ПРЕДСТАВЛЕНИЕ — представление p локально компактной группы G, индуцированное представлением р ее замкнутой подгруппы Н, точнее, представление p группы Gв нек ром пространстве Ефункций f на группе G, принимающих значения в пространстве Vпредставления р и… … Математическая энциклопедия
Регулярное деление плоскости — Эшер, Мауриц Корнелис Регулярное деление плоскости, нидерл. Regelmatige vlakverdeling Ксилография. «Регулярное деление плоскости» серия ксилографий нидерландского художника Эшера, начатая им в 1936 году. В основу этих работ лёг принцип тес … Википедия
ПРЕДСТАВЛЕНИЕ ПОЛУГРУППЫ — S в классе полугрупп X гомоморфизм полугруппы S в нек рую полугруппу из класса X (в случае изоморфизма говорят о точном представлении). Обычно имеются в виду классы каких либо конкретных полугрупп. Наиболее изучены представления в классе… … Математическая энциклопедия
УНИТАРНОЕ ПРЕДСТАВЛЕНИЕ — топологической группы представление топологич. группы унитарными операторами в гильбертовом пространстве. Теория У. п. один из наиболее разработанных разделов теории представлений топологич. групп, что связано как с его многочисленными… … Математическая энциклопедия
БЕСКОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ — группы Ли представление группы Ли в бесконечномерном векторном пространстве. Теория представлений групп Ли есть часть общей теории, представлений то пологич. групп. Специфика групп Ли позволяет использовать в этой теории средства анализа (в… … Математическая энциклопедия
ИМПРИМИТИВНАЯ ГРУППА — группа Gвзаимно однозначных отображений на себя ( подстановок )нек рого множества S, для к рой существует разбиение множества Sв объединение непересекающихся подмножеств S1, . . ., Sm, обладающее следующими свойствами: число элементов хотя бы в… … Математическая энциклопедия
ПОДСТАНОВОК ГРУППА — совокупность подстановок на нек ром множестве X, образующих группу относительно операции умножения подстановок. Иначе, П. г. это пара (G, X), где G группа, X множество и каждому соответствует подстановка множества Xтакая, что 1) , , и 2) х a=х… … Математическая энциклопедия
КОМПАКТНАЯ ГРУППА — топологическая группа, компактная как топологич. пространство. Напр., всякая конечная группа (в дискретной топологии) является К. г. Алгебраическая группа, хотя она и является компактным топологич. пространством (относительно топологии Зариского) … Математическая энциклопедия
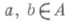; аналогично, формула 
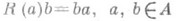, определяет (анти)-представление алгебры Ав пространстве Е=А, наз. (правым) Р. п. А. Если А - топологич. алгебра (с умножением, непрерывным по совокупности переменных), то Lи R - непрерывные представления. Если А- алгебра с единицей или полупростая алгебра, то все ее Р. п.- точные.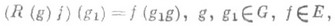
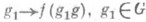, принадлежит пространству Едля всех 
. Аналогично, формула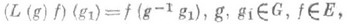 
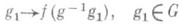, принадлежит Едля всех 
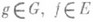. Если G - топологич. группа, то в качестве пространства Ечасто рассматриваются пространства непрерывных функций на G. Если G - локально компактная группа, то (правым) Р. п. группы G наз. (правое) Р. п. группы G в пространстве L2(G), построенном по правоинвариантной мере Хаара на G; Р. п. локально компактной группы является ее непрерывным унитарным представлением, причем левое и правое Р. п. унитарно эквивалентны. А. И. Штерн.