- ПРЯМАЯ СУММА
- конструкция, широко используемая в теориях таких математич. структур, категории к-рых близки к абелевым категориям;в неабелевом случае конструкция прямой суммы обычно наз. дискретным прямым произведением. Пусть
- нек-рый класс однотипных алгебраич. систем, содержащих одноэлементную (нулевую) подсистему. Прямой суммой или (дискретным) прямым произведением систем 
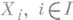, из класса U наз. подсиcтема прямого произведения
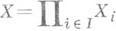, состоящая из таких функций 
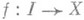, все значения к-рых, кроме конечного числа, принадлежат соответствующим нулевым подсистемам. П. с. обозначается одним из следующих способов:
Для конечного числа слагаемых используются также обозначения
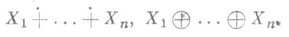
Непосредственно из определений следует совпадение П. с. и прямого произведения в случае конечности числа слагаемых.
Для каждого слагаемого П. с.
существует канонич. вложение 
, к-рое элементу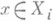 
сопоставляет функцию 
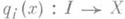, принимающую значение хпри значении аргумента iи равную нулю в остальных случаях. Следовательно, можно считать, что П. с. содержит свои слагаемые. В случае W-групп (в частности, в случае групп, абелевых групп, векторных пространств, колец) можно дать "внутреннее" определение П. с. W-группа G является П. с. своих W-подгрупп 
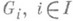, если выполнены следующие условия: a) Gпорождается 
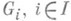; б) каждая W-подгруппа Gi является идеалом в G; в) пересечение Gi с W-подгруппой, порожденной остальными идеалами, является нулевой подгруппой для каждого i.
Всякое векторное пространство есть П. с. одномерных подпространств. Всякая свободная абелева группа является П. с. бесконечных циклич. групп. Всякая конечная абелева группа есть П. с. примерных циклич. групп. Всякое ассоциативное кольцо с единицей, удовлетворяющее условию минимальности для идеалов, есть П. с. конечного числа полных колец линейных преобразований подходящих конечномерных векторных пространств.
В теории групп, решеток и категорий глубокое развитие получила проблема изоморфизма прямых разложений, начало к-рой было положено теоремой Ремака - Шмидта о центральном изоморфизме прямых разложений групп, обладающих главным рядом (см. Крулля - Ремака - Шмидта теорема).
В теории категории иногда П. с. паз. понятие, двойственное понятию произведения, т. е. копроизведение объектов категории. М. Ш. Цаленко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
