ПРОСТРАНСТВО НАД АЛГЕБРОЙ

- пространство, обладающее дифференциально-геометрической структурой, точки к-рого могут быть снабжены координатами из нек-рой алгебры. В большинстве случаев алгебра предполагается ассоциативной с единицей, иногда - альтернативной с единицей (см. Ассоциативные кольца и алгебры, Альтернативные кольца и алгебры).

Для построения широкого класса П. н. а. можно исходить из понятия унитарного модуля над алгеброй, определение к-рого получается из определения векторного пространства над телом путем замены тела на ассоциативную алгебру с единицей (см. [1], [3]). В результате присоединения к элементам модуля, называемым векторами, новых элементов, называемых точками, связанных с векторами теми же аксиомами, что и точки аффинного пространства с его векторами, получается аффинное пространство над ассоциативной алгеброй с единицей. Аффинные преобразования в аффинном пространстве над алгеброй имеют в координатах вид

где f(x) - непрерывный автоморфизм алгебры, n-мерное аффинное пространство над алгеброй, имеющей ранг r над нек-рым полем, допускает естественную модель (представление) в nr -мерном аффинном пространстве над тем же полем. В этой модели каждая точка аффинного пространства над алгеброй изображается точкой nr -мерного аффинного пространства над рассматриваемым полем, координатами к-рой являются коэффициенты разложений координат точек пространства над алгеброй по базисным элементам алгебры. В случае, когда базисные элементы e_A, А=1, . . ., r, алгебры связаны между собой структурными уравнениями

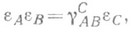
где 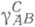- структурные константы алгебры, каждому базисному элементу e _А соответствует в модели линейное преобразование с матрицей

(*)

где по диагонали стоят n одинаковых r-мерных блоков . В аффинных пространствах над алгебрами можно задать эрмитову метрику (евклидову и псевдоевклидову), а в случае коммутативных алгебр и квадратичную (евклидову и псевдоевклидову) метрику. Для этого в унитарном модуле определяется скалярное произведение векторов ( а, b), в первом случае обладающее свойством

( а, b) = (b, а)^I,

где I - инволютивный антиавтоморфизм (инволюция) в алгебре, а во втором случае - свойством

( а, b) =(b, а).

Скалярный квадрат вектора 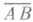определяет метрич. инварианты пары точек Аи В;движения евклидовых и псевдоевклидовых пространств - аффинные преобразования, сохраняющие скалярное произведение векторов. При замене в определении эллиптических и гиперболических П. н. а. скалярного произведения векторов скалярным произведением векторов (x, у), для к-рого (x, у)=-( у, x)^I или (x, у)=-( у, x), получается эрмитово, или квадратичное симплектическое, П. н. а.

Многообразие одномерных подмодулей (n+1 )-мерного унитарного модуля над алгеброй Кназ. n-мерным проективным пространством над алгеброй К;точками этого пространства наз. одномерные подмодули, а координаты векторов этих подмодулей наз. проективными координатами точек. В проективном П. н. а. определяются так же, как в проективных пространствах над полями, коллинеации и корреляции. В проективных координатах коллинеации имеют вид

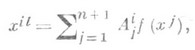
где f(х) - непрерывный автоморфизм алгебры, а корреляции имеют вид

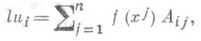
где f(x) - непрерывный антиавтоморфизм алгебры, а и _i - проективные координаты гиперплоскости. Введение скалярного произведения векторов в унитарном модуле позволяет определить в проективном пространстве, построенном с помощью этого модуля, эрмитовы или, в случае коммутативной алгебры, квадратичные эллиптические и гиперболич. метрики. Метрич. инварианты точек этих пространств определяются скалярными произведениями векторов x и y соответствующих подмодулей с помощью двойного отношения

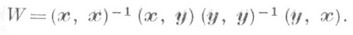
В том случае, когда W - действительное число, инвариант w, для к-рого W=cos²w, наз. расстоянием между соответствующими точками (см. [2]).

Проективные, эллиптические, гиперболические и симплектич. пространства над действительными простыми алгебрами (напр., алгебрами действительных, комплексных и кватернионных матриц) обладают тем свойством, что их фундаментальные группы являются простыми группами Ли бесконечных серий. Евклидовы, псевдоевклйдовы и квазиэллиптические, квазигиперболические и квазисимплектич. пространства над теми же алгебрами обладают тем свойством, что их фундаментальные группы являются квазипростыми группами Ли тех же серий (см. [2J); тем же свойством обладают проективные, эллиптические, гиперболические и симплектич. пространства над полупростыми алгебрами, к к-рым относится алгебра дуальных чисел.

Несколько сложнее определяются проективные и эрмитовы (эллиптические и гиперболические) плоскости над альтернативными алгебрами. Фундаментальные группы этих плоскостей являются простыми или квазипростыми группами Ли нек-рых особых классов.

Лит.:[1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [2] Розенфельд Б. А., Неевклидовы пространства, М., 1969; [3] Веnz W., Vorlesungen fiher Geometrie der Algebren, В., 1973. Б. А. Розенфельд, А. П. Широков.