ПРЕДЕЛЬНОГО ПОГЛОЩЕНИЯ ПРИНЦИП

способ однозначного выделения решений уравнений, аналогичных Гелъмголъца уравнению, с помощью введения бесконечно малого поглощения. Математич. смысл П. п. п. состоит в следующем. Пусть W - неограниченная область в , Р - самосопряженный оператор в L₂(W), задаваемый дифференциальным выражением

, и однородными граничными условиями на дW, l - точка непрерывного спектра оператора Р. Тогда при уравнение

однозначно разрешимо в L₂(W) и в нек-рых случаях можно выделить решения u=u₊ уравнения

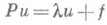
с помощью предельного перехода

При этом предполагается, что f имеет компактный носитель, а сходимость при 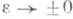понимается в смысле L₂(W'), где W' - произвольная ограниченная область в W. Так как l - точка спектра оператора Р, то указанный предел в L₂(W), вообще говоря, не существует.

Впервые П. п. п. был сформулирован для уравнения Гельмгольца в (см. [1]):

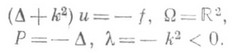
Выделяемые с помощью этого принципа решения и ₊ соответствуют расходящимся или сходящимся волнам и удовлетворяют излучения условию на бесконечности. Эти результаты были перенесены (см. [2], [3]) на эллиптические краевые задачи во внешности ограниченной области в для оператора

(*)

где коэффициенты а _ki(x) достаточно быстро стремятся к константам при . Для справедливости П. п. п. в этом случае необходимо требовать, чтобы l не было собственным значением оператора Рили f была ортогональна собственным функциям. Теорема Като (см. [3]) дает достаточные условия отсутствия собственных значений на непрерывном спектре оператора Р=D+q (х). Такая теорема получена для оператора (*) (см. [3]). П. п. п. обоснован для нек-рых областей с некомпактной границей (см. [3], [4]).

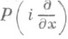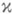П. п. п. и соответствующие условия излучения найдены для уравнений любого порядка и систем уравнений (см. [5], [6]); они состоят в следующем. <Пусть - эллиптический (или гипоэллиптический) оператор, удовлетворяющий условиям: 1) многочлен Р(s) имеет действительные коэффициенты, 2) поверхность Р(s)=0, , распадается на -связных гладких поверхностей S_j с отличной от нуля кривизной, 3) gradР(s)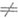0 на S_j. Пусть на Sj заданы ориентации, т. е. независимо для каждой поверхности выбраны направления нормали v. Пусть - точка на S_j, в к-рой v и w имеют одинаковые направления, и m_j(w)=(s_j(w),w). Тогда функция и(х).удовлетворяет условиям излучения, если она представима в виде

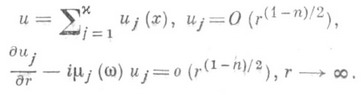
Эти условия выделяют единственное решение уравнения

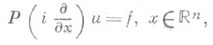
для любой функции f с компактным носителем. П. п. п. для этого уравнения заключается в том, что это же решение получается в пределе при 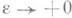из однозначного определяемого решения 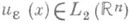эллиптич. уравнения

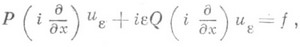
где Q(s) имеет действительные коэффициенты и Q(s)0 на S_j. В зависимости от набора

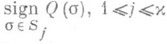, в пределе получаются решения с условиями излучения, соответствующими той или иной ориентации поверхностей S_j. Этот принцип обоснован для уравнений и систем любого порядка с переменными коэффициентами во внешности ограниченной области (см. [5], [6]), а также в случае невыпуклых S_j;для этих уравнений имеется и теорема единственности типа Като.

Лит.:[1] Игнатовский B.C., "Ann. Phys.", 1905, Bd 18, № 13, S. 495-522; [2] Повзнер А. Я., "Матем. сб.", 1953, т. 32, № 1, с. 109-56; [3] Эйдус Д. М., "Успехи ма-тем. наук", 1969, т. 24, в. 3, с. 91-156; [4] Свешников А. Г., "Докл. АН СССР", 1951, т. 80, № 3, с. 345-47; [5] Вайнберг Б. Р., "Успехи матем. наук", 1966, т. 21, в. 3, с. 115-94; [6] его ж е, "Матем. сб.", 1968, т. 75, №3, с. 454-80.

В. Р. Вайнберг.