ПРЕДЕЛЬНОЙ АМПЛИТУДЫ ПРИНЦИП

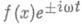способ однозначного выделения решений стационарных уравнений, описывающих установившиеся колебания, через предел при амплитуды решений соответствующих нестационарных уравнений с нулевыми начальными данными и периодической по tправой частью вида . Справедливость П. а. п. означает, что решение v(x, t).указанной нестационарной задачи при 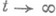имеет вид 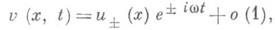(*) где u₊ - решения стационарного уравнения.

Впервые этот принцип был предложен (см. [1]) для уравнения Гельмгольца в (D + k²)u = f, он выделяет те же решения этого уравнения, что и излучения условия и предельного поглощения принцип. Справедливость П. а. п. исследована: для уравнений 2-го порядка с переменными коэффициентами во внешности ограниченной области (см. [2], [3]), уравнения Гельмгольца в нек-рых областях с некомпактной границей (см. [3], [4]), задачи Коши - Пуассона в полосе (см. [5]), нек-рых уравнений высокого порядка (см. [3], [6]), смешанных задач во внешности ограниченной области для уравнений и систем любого порядка с переменными коэффициентами (см. [7]). В последнем случае условия излучения и принцип предельного поглощения выделяют , решений стационарного уравнения, а П. а. п. дает два из них. Указаны (см. [8]) такие постановки П. а. п., к-рые позволяют получить все эти решений.

Для справедливости П. а. п. необходимо, чтобы f(х).была ортогональна всем собственным функциям стационарной задачи. Поэтому П. а. п. не справедлив в ограниченной области. Пусть -Р_l - оператор, к-рый соответствует зависящей полиномиально от спектрального параметра l. стационарной задаче, полученной из смешанной задачи для нестационарного уравнения заменой в уравнении и граничных условиях оператора дифференцирования iд/дt на параметр Я. Справедливость для оператора Р _l; l=const, П. а. п. связана с возможностью аналитич. родолжения ядра резольвенты на непрерывный спектр и гладкостью по l. этого продолжения (см. [3], [7]). Если ядро R_l допускает аналитич. родолжение через непрерывный спектр и имеет подходящие оценки при 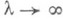, то можно написать асимптотику при остатка 0 (1) в (*), а также получить асимптотику при решений других нестационарных задач (см. [2], [7]). Указанные свойства R_l получены в [7] для смешанных задач во внешности ограниченной области для уравнений и систем любого порядка.

Лит.:[1] Тихонов А. Н., Самарский А. А., "Ж. эксперимент, и теоретич. физики", 1948, т. 18, № 2, с. 243-248; [2] Ладыженская О. А., "Успехи матем. наук", 1957, т. 12, в. 3, с. 161-64; [3] Эйдус Д. М., там же, 1969, т. 24, в. 3, о. 91-156; [4] Свешников А. Г., "Докл. АН СССР", 1950, т. 73, № 5, с. 917-20; [5] Исакова Е. К., "Дифференциальные уравнения", 1970, т. 6, № 1, с. 56-71; [6] Михайлов В. П., "Тр. Матем. ин-та АН СССР", 1967, т. 91, с. 100-12; [7] Вайнберг Б. Р., "Успехи матем. наук", 1975, т. 30, в. 2, с. 3-55; [8] его же, "Изв. ВУЗов. Математика", 1974, Ni 2, с. 12-23. Б. Р. Вайнберг.