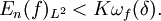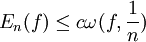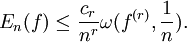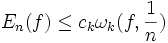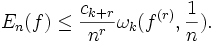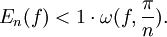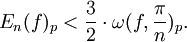Неравенство Джексона — Стечкина

Неравенство Джексона — Стечкина

Неравенство Джексона — Стечкина связывает величину наилучшего приближения функции каким либо классом функций со свойствами этой функции, как правило со значением модуля непрерывности этой функции в определенной точке. Пример:

$E_n(f)_{L^2}< K \omega_{f}(\delta).$

В примере величина наилучшего приближения функции f полиномами степени n в пространстве L² оценивается сверху через значение модуля непрерывности функции f в точке δ. Величина K называется константой Джексона. Вопрос о наименьшем значении этой величины (о «точной константе Джексона»), как правило, очень труден. В тех случаях, когда он разрешим, минимальная константа δ, при которой неравенство остается справедливым, называется точкой Черных, нахождение которой также является нетривиальным.

История

Впервые неравенство такого типа было получено Д. Джексоном (Dunham Jackson) в 1911 году для случая приближения периодических функций тригонометрическими полиномами. Он показал, что

$E_n(f) \le c \omega(f, \frac1n)$

и

$E_n(f) \le \frac{c_r}{n^r} \omega(f^{(r)}, \frac1n).$

Здесь E_n(f) есть величина наилучшего приближения функции f в равномерной метрике тригонометрическими полиномами степени n − 1. В первом неравенстве функция f предполагается непрерывной, а во втором — r-раз дифференцируемой. В 1945 году Зигмунд получил подобные неравенства с использованием модуля непрерывности второго порядка, в 1947 году академик С. Н. Бернштейн смог использовать модуль непрерывности порядка k. В 1949 году С. Б. Стечкин обобщил все предыдущие результаты и установил (отличным от Джексона методом), что

$E_n(f) \le c_k \omega_k(f, \frac1n)$

и

$E_n(f) \le \frac{c_{k+r}}{n^r} \omega_k(f^{(r)}, \frac1n).$

Здесь константы c_k не зависят от f, n или r. В результате в отечественной литературе неравенство стало называться неравенством Джексона-Стечкина, а похожие неравенства стали называться неравенствами типа Джексона-Стечкина.

В 1961 году Н.П. Корнейчук указал точную константу Джексона в первом неравенстве:

$E_n(f) < 1 \cdot \omega(f, \frac{\pi}{n}).$

В 1967 году Стечкин получил неравенство Джексона в пространствах L_p для всех $p \in [1, \infty)$:

$E_n(f)_p < \frac{3}{2} \cdot \omega(f, \frac{\pi}{n})_p.$

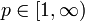Позднее этой тематикой занималось (и до сих пор занимаются) большое число математиков в разных странах, были получены аналогичные неравенства для разнообразных пространств, приближающих классов и модулей непрерывности.