ПОПОЛНЕНИЕ СЕЧЕНИЯМИ

, пополнение Мак-Нейла, частично упорядоченного множества М - полная решетка L, получаемая из множества Мследующим образом. Пусть 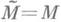(если Мобладало нулем) или получается внешним присоединением наименьшего элемента 0 к М(если Мне имело нуля). И пусть Р(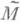) - упорядоченное отношением включения множество всех непустых подмножеств множества 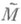. Для любого 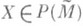пусть

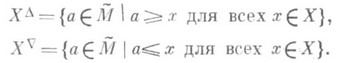
Условие 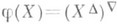определяет замыкания отношение ф на множестве Р(). Решетка Lвсех ф-замкнутых подмножеств множества Р(М).является полной. Для любого множество является главным идеалом, порожденным элементом х. Полагая i(x)=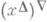 для всех , получают изоморфное вложение iмножества Мв полную решетку L, сохраняющее все точные верхние и нижние грани, существующие в М. В применении к упорядоченному множеству рациональных чисел описанная конструкция дает пополнение множества рациональных чисел дедекиндовыми сечениями.

Лит.:[1] Масnеillе Н. М., "Trans. Amer. Math. Soc.", 1937, v. 42, p. 416-60. Т. С. Фофанова.