ПОПОЛНЕНИЕ РАВНОМЕРНОГО ПРОСТРАНСТВА

X - отделимое полное равномерное пространство 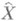такое, что существует равномерно непрерывное отображение и для любого равномерно непрерывного отображения f пространства X в отделимое полное равномерное пространство Y существует, и притом единственное, равномерно непрерывное отображение , причем f=goi. Подпространство i(X).плотно в , и образы при отображении iXi окружении для Xявляются окружениями для i(X), а замыкания последних в образуют фундаментальную систему окружений для . Когда Xотделимо, iинъективно (что позволяет отождествить X с i(X). Отделимое пополнение подпространства изоморфно замыканию . Отделимое пополнение произведения равномерных пространств изоморфно произведению отделимых пополнений пространств-сомножителей.

Доказательство существования по существу обобщает построение Г. Кантора (G. Cantor) множества действительных чисел из чисел рациональных.

Лит.:[1] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968. М. И. Войцеховский.