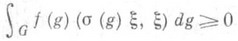ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ
- ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ
комплекснозначная функция j на группе G, удовлетворяющая неравенству
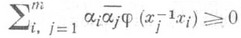
для любых наборов  Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения.
Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения.
Причина выделения этого класса функций состоит в том, что именно П. о. ф. определяют положительные функционалы на групповой алгебре  и унитарные представления группы G. Точнее, пусть
и унитарные представления группы G. Точнее, пусть  - произвольная функция и
- произвольная функция и  - функционал, заданный равенством
- функционал, заданный равенством
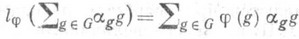
тогда для положительности fj необходимо и достаточно, чтобы j была П. о. ф. Далее, fj определяет *-представление алгебры  в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем
в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем  для нек-рого
для нек-рого  . Обратно, Для любого представления p и любого вектора
. Обратно, Для любого представления p и любого вектора 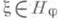 функция
функция  является П. о. ф.
является П. о. ф.
Если G- топологич. группа, то представление pj слабо непрерывно тогда и только тогда, когда П. о. ф. непрерывна. Если Gлокально компактна, то непрерывные П. о. ф. взаимно однозначно соответствуют положительным функционалам на L1(G).
Для коммутативных локально компактных групп класс П. о. ф. совпадает с классом преобразований Фурье конечных положительных мер на двойственных группах. Имеется аналог этого утверждения для компактных групп: непрерывная функция j на компактной группе Gявляется П. о. ф. тогда и только тогда, когда ее преобразование Фурье  принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.
принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.
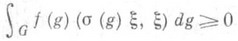
для всякого представления s и всякого вектора 
Лит.:[1] Xьюитт Э., Росс К., Абстрактный гармонический анализ, пер. с англ., т. 2, М., 1975; [2] Наймарк М. А., Нормированные кольца, 2 изд., М., 1968.
В. С. Шулъман.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ ФУНКЦИЯ" в других словарях:
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННОЕ ЯДРО — комплекснозначная функция K на , где X произвольное множество, удовлетворяющая условию для любых . Измеримые П. о. я. на пространстве с мерой (X,m) соответствуют положительным интегральным операторам в L2 (X,m); включение в схему такого… … Математическая энциклопедия
УСТОЙЧИВОСТЬ ПО ЧАСТИ ПЕРЕМЕННЫХ — устойчивость в смысле Ляпунова решения х=0по отношению не ко всем, а лишь к нек рым переменным x1, . . .. xk, k< п, системы обыкновенных дифференциальных уравнений Здесь Xs(t, x) данные действительные непрерывные функции, удовлетворяющие в… … Математическая энциклопедия
УНИТАРНОЕ ПРЕДСТАВЛЕНИЕ — топологической группы представление топологич. группы унитарными операторами в гильбертовом пространстве. Теория У. п. один из наиболее разработанных разделов теории представлений топологич. групп, что связано как с его многочисленными… … Математическая энциклопедия
ХАРАКТЕР — представления группы G в случае конечномерного представления функция на группе G,определяемая формулой Для произвольных непрерывных представлений топологич. группы G над полем С это определение обобщается следующим образом: где линейный… … Математическая энциклопедия
ОБОБЩЕННОГО СДВИГА ОПЕРАТОРЫ — гипергруппа, понятие, возникшее в результате аксиоматизации нек рых свойств операторов сдвига в пространствах функций на группе. В терминах операторов группового сдвига можно сформулировать такие важные математич. понятия как свертка, групповая… … Математическая энциклопедия
ГИЛЬБЕРТА ТЕОРИЯ — 1) Г. т. о базисе: если А коммутативное нётерово кольцо и кольцо многочленов от с коэффициентами в А, то и нётерово кольцо. В частности, в кольце многочленов от конечного числа переменных над полем или над кольцом целых чисел любой идеал… … Математическая энциклопедия
ПОЛОЖИТЕЛЬНОЕ РАССЛОЕНИЕ — обобщение понятия дивизора положительной степени на римановой поверхности. Голоморфное векторное расслоение Енад комплексным пространством Xназ. положительным (обозначается E>0), если в Есуществует такая эрмитова метрика h, что функция на… … Математическая энциклопедия
СЛУЧАЙНОЕ ПОЛЕ ОБОБЩЕННОЕ — обобщенный случайный процесс, случайная функция на гладком многообразии G, типичными реализациями к рой являются обобщенные функции, заданные на этом многообразии G. Точнее, пусть G бесконечногладкое многообразие и D(G) пространство бесконечно… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия
Унитарное пространство — Унитарное пространство векторное пространство над полем комплексных чисел с эрмитовым скалярным произведением. Эрмитовым скалярным произведением в линейном пространстве над полем комплексных чисел называется функция удовлетворяющая… … Википедия
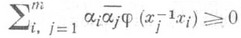
 Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения.
Совокупность П. о. ф. на G образует конус в пространстве М(G).всех ограниченных функций на G, замкнутый относительно операций умножения и комплексного сопряжения. и унитарные представления группы G. Точнее, пусть
и унитарные представления группы G. Точнее, пусть  - произвольная функция и
- произвольная функция и  - функционал, заданный равенством
- функционал, заданный равенством 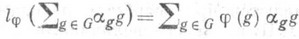
 в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем
в гильбертовом пространстве Hj и, следовательно, унитарное представление pj группы G, причем  для нек-рого
для нек-рого  . Обратно, Для любого представления p и любого вектора
. Обратно, Для любого представления p и любого вектора 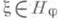 функция
функция  является П. о. ф.
является П. о. ф. принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.
принимает положительные (операторные) значения на каждом элементе двойственного объекта, т, е.