БЕРЕНСА - ФИШЕРА ПРОБЛЕМА

аналитическая проблема, возникшая в связи со статистич. задачей сравнения по эмпирич. данным математич. ожиданий в двух нормальных распределениях, дисперсии к-рых неизвестны (предполагается, что отношение дисперсий также неизвестно). Эта задача была поставлена В. Бе-ренсом [1] в связи с вопросом обработки данных об урожайности. Современная формулировка Б.- Ф. п. принадлежит Р. Фишеру (R. Fisher) и основана на понятии достаточной статистики. Пусть - взаимно независимые случайные величины, распределенные нормально, причем . Предполагается, что значения математич. ожиданий 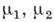, дисперсий , а также их отношения неизвестны. Достаточная статистика в случае есть четырехмерный вектор , компоненты к-рого выражаются формулами

и представляют собой взаимно независимые случайные величины, причем подчиняются стандартному нормальному распределению, а 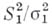и - распределению хи-квадрат с и степенями свободы соответственно. Поскольку доста-.точная статистика несет в себе ту же информацию о неизвестных параметрах что и исходные случайные величины в количестве то при проверке гипотез о значениях этих параметров разумно рассматривать лишь достаточную статистику. В частности, это соображение служит основой современной формулировки задачи о проверке гипотезы, согласно к-рой ( - заранее заданное число); при этом Б.- Ф. п. заключается в отыскании такого множества 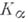в пространстве возможных значений случайных величин чтобы при справедливости проверяемой гипотезы вероятность события не зависела от всех неизвестных параметров и в точности равнялась наперед заданному Числу из интервала .

Вопрос о существовании решения В.- Ф. п. долгое время дискутировался видными математиками (главным образом в связи с предложенным Р. Фишером подходом к этой проблеме, по существу выходящим за рамки теории вероятностей). В 1964 Ю. В. Линник (совместно с учениками) доказал, что при объемах выборок и п ₂ разной четности решение В.- Ф. п. существует. Вопрос же о существовании решения для 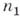и одинаковой четности остался открытым.

Б.- Ф. п. неоднократно подвергалась видоизменениям и обобщениям. В частности, А. Вальд (A. Wald) предложил задачу об отыскании множества К _a. в пространстве двух церемонных . Вопрос о существовании такого решения остается открытым. Однако можно эффективно построить такое множество , что в случае справедливости проверяемой гипотезы вероятность события хотя и будет зависеть от неизвестного отношения 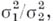но ее отклонение от заданного будет мало. Это обстоятельство и служит основой современных рекомендаций для практич. построения критериев сравнения .

Простые и удобные в вычислительном отношении критерии для сравнения 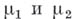предложены В. И. Романовским, М. Бартлеттом (М. Bartlett), Г. Шеффе (Н. Scheffe) и др. Однако статистики этих критериев в терминах достаточной статистики не выражаются и поэтому имеют, вообще говоря, меньшую мощность, чем критерии, конструируемые с помощью решения Б.- Ф. п. и ее обобщений.

Лит.: [1] Behrens W. U., "Landwirtsch. Jahr".", 1929, Bd 68, №. 6, S. 807-37; [2] Линник Ю. В., Статистические задачи с мешающими параметрами, М., 1966; [3] Линник Ю. В., Романовский И. В., Судаков В. Н., "Докл. АН СССР", 1964, т. 155, № 6, с. 1262 - 64. Л. Н. Большее.

ВЁРКИЛЯ ИНТЕГРАЛ - понятие, введенное Дж. Бёркилем [1] для определения площади поверхности. В современном виде Б. и. вводится для интегрирования неаддитивной функции re-мерного сегмента (бруса). Пусть R есть множество, представимое в виде суммы (объединения) конечного числа сегментов (такое множество наз. фигурой). Каждое представление наз. разбиением фигуры R. Верхним Б. и. и нижним Б. и. от функции сегмента 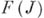по фигуре Rназ. соответственно верхний и нижний пределы сумм для всевозможных разбиений при стремлении к нулю максимума диаметров сегментов, входящих в разбиение. Если эти интегралы равны, то их общее значение наз. интегралом Бёркиля от функции по и обозначается . Если Fинтегрируема на R, то Fинтегрируема на каждой фигуре . Тем самым вводится неопределенный Б. и., к-рый является аддитивной функцией множества. Если Fнепрерывна, то и неопределенный Б. и. непрерывен.

Понятие Б. и. может быть обобщено на случай функции множества, определенной на нек-ром классе подмножеств абстрактного пространства с мерой. Этот класс должен удовлетворять ряду требований; в частности, каждое множество из данного класса должно допускать разбиение на составляющие множества из того же класса, имеющие произвольно малые меры. Тогда для любого множества из класса определяется Б. и. по аналогии с n-мерным случаем, причем соответствующие пределы берутся при стремлении к нулю максимума мер составляющих множеств. Б. и. естественным образом обобщается на функции множества со значениями в коммутативной топологич. группе. Б. и. является менее общим, чем введенный позднее Колмогорова интеграл, наз. также интегралом Бёркиля - Колмогорова. Всякая интегрируемая по Бёркилю функция интегрируема по Колмогорову при соответствующем упорядочении разбиений. Обратное верно лишь при нек-рых дополнительных условиях. Б. и. используется для построения Данжуа интеграла в различных пространствах.

Интегралом Бёркиля наз. также ряд введенных Дж. Бёркилем обобщений Перрона интеграла( АР- интеграл СР- интеграл, SCP- интеграл), в определении к-рых вместо обычных производных чисел используются нек-рые обобщенные производные числа. Эти Б. и. находят применение в теории тригонометрич. рядов.

Лит.:[1] Burkill J. С., "Ргос. London Math. Soc.", ser. 2, 1924, v. 22, p. 275-336; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949; [3] Романовский П. И., "Матем. сб.", 1941, т. 9, №1, с. 67-120; [4] Вurki11 J. С., "Ргос. London Math. Soc.", ser. III, 1951, v. 1, № 1, p. 46-57.

В. А. Скворцов.