ПОЛИЭДР

- объединение локально конечного семейства выпуклых многогранников в нек-ром Rⁿ. Под выпуклым многогранником понимается пересечение конечного числа замкнутых полупространств в случае, если это пересечение ограничено. Локальная конечность семейства означает, что каждая точка 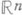имеет окрестность, пересекающуюся лишь с конечным числом многогранников. Компактный П. является объединением конечного числа выпуклых многогранников. Размерность П. определяется как максимальная размерность составляющих его многогранников. Любое открытое подмножество П., в частности любое открытое подмножество евклидова пространства, есть П. Полиэдрами являются также конус и надстройка над компактным П. Простые примеры (конус над интервалом) показывают, что соединение компактного и некомпактного П. может не быть П. Подполиэдром полиэдра Qназ. любой полиэдр Р, лежащий в Q. Иногда ограничиваются рассмотрением только замкнутых подполиэдров. 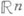Каждая точка а полиэдра обладает в Рокрестностью, являющейся конусом в с вершиной а и с компактным основанием. Это свойство оказывается характеристическим: любое подмножество 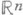, каждая точка к-рого имеет конич. окрестность с компактным основанием, является П.

Каждый компактный полиэдр Рможно так разбить на конечное число замкнутых симплексов, чтобы каждые два симплекса либо не пересекались, либо пересекались по их общей грани. В случае некомпактного П. требуется, чтобы семейство симплексов было локально конечным. Такое разбиение наз. прямолинейной триангуляцией П. Любые две триангуляции одного и того же П. имеют общее подразделение. Если Р - замкнутый подполиэдр полиэдра Q, то любая триангуляция Кполиэдра Рпродолжается до нек-рой триангуляции Lполиэдра Q. В этом случае говорят, что получающаяся пара (L, К).геометрических симплициальных комплексов триангулирует пару (Q, Р). Отображение f полиэдра 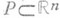в полиэдр 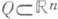наз. кусочно линейным, или pl -отображением, если f является симшгациаль-ным в нек-рых триангуляциях полиэдров Ри Q. Эквивалентное определение: f кусочно линейно, если f локально коническое, т. е. если каждая точка имеет такую конич. 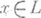окрестность N=a*L, что f (la+mx)=lf(а)+mf(x) при любых и 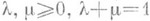Для того чтобы отображение f было кусочно линейным, необходимо и достаточно, чтобы его график 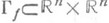являлся П. Суперпозиция кусочно линейных отображений кусочно линейна. Обратное отображение к обратимому кусочно линейному отображению f кусочно линейно. В этом случае f наз. pl- гомеоморфизмом.

Категория, объектами к-рой являются П. (и полиэдральные пары), а морфизмами являются pl -отображе-ния, обозначается PL или 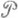(см. также Кусочно линейная топология). Категория PL является одним из основных объектов и инструментов исследования в топологии. Особенно велика роль категории PL в алгебраической топологии и топологии многообразий. Это объясняется тем, что класс П. достаточно широк.

Напр., каждое дифференцируемое многообразие можно естественным образом представить в виде П. Каждое непрерывное отображение одного П. в другой сколь угодно точно аппроксимируется pl -отображением. Поэтому категория PL является хорошим приближением к категории всех топологич. пространств и непрерывных отображений. С другой стороны, триангулируемость П. позволяет использовать методы комбинаторной топологии. Многие алгебраич. инварианты (напр., гомологии группы, когомологий кольцо).строятся и эффективно вычисляются с помощью разбиения на симплексы. Вопрос о том, всякие ли гомеоморфные полиэдры pl -гомеоморфны, носит название основной гипотезы и решается отрицательно: для п 5 существуют гомеоморфные, но не рl -гомеоморфные n-мерные П. (см. [3]). При п 3 гомеоморфные n-мерные полиэдры pl -гомеоморфны, при n=4 вопрос остается (1983) открытым для компактных П. и решается отрицательно для некомпактных: существует нестандартная pZ-структура на 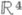. Полиэдр Мназ. и-мерным pl- многообразием, если каждая его точка имеет окрестность, pl -гомеоморфную 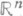или 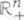. Всякая прямолинейная триангуляция T pl -многообразия Мкомбинаторна. Это означает, что звезда каждой ее вершины комбинаторно эквивалентна симплексу. Основная гипотеза для П., являющихся n-мерными топологич. многообразиями, естественно распадается на две гипотезы: гипотезу о комбинаторности всякой триангуляции такого П. и основную гипотезу для pl- многообразий. Одним из важнейших достижений современной топологии является отрицательный ответ на обе гипотезы для n5 (см. [4], [5]). Для п 3 обе гипотезы справедливы.

Пусть Р - компактный подполиэдр полиэдра Qи пусть пара геометрических симплициальных комплексов (L, К).триангулирует пару (Q, P).так, что К- полный подкомплекс. Это означает, что каждый симплекс комплекса L, вершины к-рого лежат в К, лежит в К, и этого всегда можно добиться с помощью перехода к производному подразделению. Полиэдр N, состоящий из всех замкнутых симплексов производного подразделения L', имеющих вершину в К, а также его образ при любом неподвижном на Р рl -гомеоморфизме Qна себя, наз. регулярной окрестностью полиэдра Рв полиэдре Q. Для любых двух регулярнык окрестностей N₁, N₂ полиэдра Рсуществует неподвижная на Р рl -изотопия 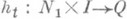, переводящая N₁ в N₂, т. е. такая, что h₀(N₁)=N₁ и h₁(N₁)=N₂. Говорят, что полиэдр Р получается элементарным полиэдральным стягиванием полиэдра , если для нек-рого nО пара (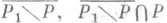) pl -гомеоморфна паре (,). Полиэдр P₁ полиэдрально стягивается на свой подполиэдр Р ( обозначение()), если от P₁ к Рможно перейти конечной последовательностью элементарных полиэдральных стягиваний. Если , то в нек-рой триангуляции пары ( Р ₁, Р).полиэдр Р можно получить из P₁ последовательностью элементарных комбинаторных стягиваний, каждое из к-рых состоит в отбрасывании главного симплекса вместе с его свободной гранью. Если Qявляется n-мерным pl -многообразием, то любая регулярная окрестность компактного подполиэдра является n-мерным pl -многообразием и полиэдрально стягивается на Р. Это свойство оказывается характеристическим: если n-мерное pl -многообразие таково, что Р Int Nи , то N - регулярная окрестность Р. При этом любая регулярная окрестность края дМ- компактного pl -многообразия М pl -гомеоморфна дМI.

Пусть Р, Q - замкнутые подполиэдры n-мерного pl -многообразия М,dim Р=р, dim Q=q. Говорят, что Ри Qнаходятся в общем положении, если 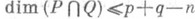. Любые замкнутые подполиэдры 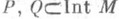можно привести в общее положение сколь угодно малой изотонией М. Это означает, что для любого e>0 существует такая (e- рl )-изотопия h_t:М М, что полиэдры Ри Q₁=h₁(Q).находятся в общем положении. Иногда в определение общего положения включают условия типа трансверсальности. Напр., если p--q=n, то можно добиться, чтобы для каждой точки и нек-рой окрестности Uточки а в Мтройка () была pl -гомеоморфна тройке

Кривой, или топологический, П.- топологич. пространство X, снабженное гомеоморфизмом , где Ресть П. Образы симплексов какой-либо триангуляции Тполиэдра Робразуют криволинейную триангуляцию X. Говорят также, что гомеоморфизм f задает на X pl-c труктуру. Две pl -структуры , i=1, 2, совпадают, если гомеоморфизм кусочно линеен, изотопны, если гомеоморфизм 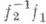изотопен кусочно линейному, и эквивалентны, если Р ₁ и Р ₂ pl -гомеоморфны. Для любого дифференцируемого многообразия Мсуществует pl -структура f : Р 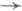М, согласованная с дифференцируемой структурой на М. Это означает, что для каждого замкнутого симплекса sнек-рой триангуляции полиэдра Ротображение дифференцируемо и не имеет особых точек. Любые две такие pl- структуры на Мизотопны. Все понятия, определяемые для П. (триангуляция, подполиэдр, регулярная окрестность, общее положение), переносятся с помощью гомеоморфизма 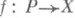на криволинейный полиэдр X.

Лит.: [1] Александров П. С., Комбинаторная топология, М.- Л., 1947; [2] Рурк К., Сандерсон Б., Введение в кусочно линейную топологию, М.. 1974; [3] Мi1nоr J., "Ann. Math.", 1961, v. 74, № 3, p. 575; [4] Кirbу R., Siebenmann L., "Ann Math. Stud.", 1977, № 88; [5] Edwards R., "Notices A. M. S.", 1975, v. 22, № 2, p. A-334.

С. В. Матвеев.