- ГРАФИК
отображения
множества 
во множество Y - подмножество 
произведения 
, состоящее из точек вида 
), 
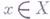. Если 
- топологич. пространства, f - непрерывное отображение и 
- проекция топологич. произведения 
на сомножитель X, то на подпространстве Г произведения 
отображение рявляется гомеоморфизмом. Если пространство Yхаусдорфово, то множество Г замкнуто в произведении 
. Б. А. Пасынков.
В случае действительной функции f с n действительными аргументами
и областью определения 
график есть множество всех упорядоченных нар 
где 
- любая точка из 
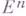; иначе - множество всех точек (
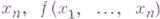) пространства 
. Если выбрать систему координат (прямоугольную декартову, полярную или какую-либо другую), то числовые точки 
можно изобразить точками плоскости или пространства. Для действительных функций 
одного действительного переменного, имеющих 
в более или менее сложных примерах эскиз Г. строится при помощи исследования знака 
и 
. По знаку 
судят о монотонности функции f, по знаку 
- о направлении выпуклости Г. функции. Для получения представления о графике действительной функции 
двух действительных переменных может применяться метод сечений: рассматриваются сечения Г. нек-рыми плоскостями, в частности, плоскостями z=c;проекция этого сечения на плоскость Оху наз. множеством уровня функции 
Аналогично, для функций 
с областью определения 
множеством уровня функции 
с 
(с - любое число) наз. множество всех решений уравнения 
; решения 
нужно искать в Е n. Множество уровня может оказаться пустым множеством. Если множество уровня есть линия или поверхность, то она наз. линией или поверхностью уровня функции. А. А. Конюшков.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
