- ПОДРАЗДЕЛЕНИЕ
геометрического с и м-плициального комплекса К - такой геометрический симплициальный комплекс К г, что тело KI совпадает с телом К и каждый симплекс К г содержится в нек-ром симплексе К. Практически переход к П. производится с помощью разбиения симплексов комплекса Кна более мелкие симплексы так, чтобы разбиение каждого симплекса было согласовано с разбиением его граней. В частности, каждая вершина Кявляется вершиной К^. Переход к П. обычно используется для доказательства инвариантности комбинаторно определяемых характеристик полиэдров (напр., эйлеровой характеристики, гомологии групп), а также для получения триангуляции с нужными свойствами (напр., достаточно мелких триангуляции). Звездное П. комплекса К с центром в точке
 получается следующим образом. Замкнутые симплексы К,: не содержащие точку а, остаются без изменения. Каждый замкнутый симплекс а, содержащий точку а, разбивается на конусы с вершиной в точке анад теми гранями о, к-рые не содержат а. Для любых двух триангуляции 7, T^ одного и того же полиэдра Рсуществует триангуляция Т 3 полиэдра Р, получающаяся как из Т 1: так и из Т 2 последовательностью звездных П. Понятие звездного П. допускает формализацию на языке абстрактных симплициальных комплексов (сим-плициальных схем). Любое звездное П. замкнутого подкомплекса продолжается до звездного П. всего . комплекса. П р о и з во дное подразделение К' комплекса Кполучается в результате последовательных звездных П. с центрами во всех открытых симплексах Кв порядке убывания их размерностей. Для произвольного замкнутого подкомплекса Ккомплекса Lподкомплекс
получается следующим образом. Замкнутые симплексы К,: не содержащие точку а, остаются без изменения. Каждый замкнутый симплекс а, содержащий точку а, разбивается на конусы с вершиной в точке анад теми гранями о, к-рые не содержат а. Для любых двух триангуляции 7, T^ одного и того же полиэдра Рсуществует триангуляция Т 3 полиэдра Р, получающаяся как из Т 1: так и из Т 2 последовательностью звездных П. Понятие звездного П. допускает формализацию на языке абстрактных симплициальных комплексов (сим-плициальных схем). Любое звездное П. замкнутого подкомплекса продолжается до звездного П. всего . комплекса. П р о и з во дное подразделение К' комплекса Кполучается в результате последовательных звездных П. с центрами во всех открытых симплексах Кв порядке убывания их размерностей. Для произвольного замкнутого подкомплекса Ккомплекса Lподкомплекс  - полный в следующем смысле: из того, что все вершины нек-рого симплекса
- полный в следующем смысле: из того, что все вершины нек-рого симплекса  лежат в К', следует, что
лежат в К', следует, что 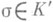 . Если в качестве центров производного П. выбрать барицентры симплексов, то получится барицентрическое П. Если диаметр каждого симплекса n-мерного комплекса Кне превосходит числа d, то диаметры симплексов его барицентрического П. ограничены числом
. Если в качестве центров производного П. выбрать барицентры симплексов, то получится барицентрическое П. Если диаметр каждого симплекса n-мерного комплекса Кне превосходит числа d, то диаметры симплексов его барицентрического П. ограничены числом 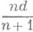 . Диаметры симплексов m-кратного барицентрического П. комплекса Кограничены числом
. Диаметры симплексов m-кратного барицентрического П. комплекса Кограничены числом 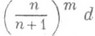 , т. е. могут быть сделаны сколь угодно малыми путем выбора достаточно большого т.
, т. е. могут быть сделаны сколь угодно малыми путем выбора достаточно большого т.
Лит.:[1] Александров П. С., Комбинаторная топология, М.- Л., 1947; [2] Хилтон П. - Д ж., Уайли С., Теория гомологии. Введение в алгебраическую топологию, пер. с англ., М., 1966. С. В. Матвеев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
