БЕМОЛЬНАЯ НОРМА

-мерной полиэдральной цепи Ав пространстве Е ⁿ - норма , определяемая следующим образом:

,

где - масса цепи - ее граница, и нижняя грань берется по всем -мерным полиэдральным цепям. Свойства Б. н.:

для любой клетки , если - проекция на нек-рую плоскость, то .

Пополнение линейного пространства полиэдральных цепей является сепарабельным банаховым пространством ; элементы его наз. -мерными бемольными цепями, и каждой из них можно приписать конечную или бесконечную массу:

Граница бемольной цепи также определяется предельным переходом, она является непрерывной операцией, и

Б. н. представляет собой наибольшую из полунорм 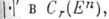удовлетворяющую для любой клетки неравенствам: г-мерная бемольная коцепь X - линейная функция r-мерных бемольных цепей А(обозначается через X^. А) такая, что ( - комасса X)

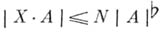
для нек-рого N.

Она является элементом сопряженного с пространства , к-рое оказывается несепарабельным.

Бемольная норма -мерной бемольной коцепи Xопределяется стандартным образом:

так что

причем

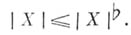
Для кограницы бемольной коцепи (определяемой условием: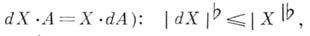 так что

Аналогичные понятия вводятся для полиэдральных r-мерных цепей, расположенных в открытых подмножествах 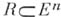. См. также Бемольная форма.

Лит.:[1] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960. М. И. Войцеховский.