ПЕРЕНОСА ИЗЛУЧЕНИЯ ТЕОРИЯ

исследование прохождения электромагнитного излучения, гамма-квантов, нейтронов и др. элементарных частиц через вещество с помощью линейного кинетического уравнения, или уравнения переноса (см. Кинетическое уравнение).

Задача определения поля излучения в атмосфере, рассеивающей свет по известным физич. законам, возникла в 80-е гг. 19 в. в связи с исследованиями по освещенности дневного неба. Кинетич. уравнение переноса излучения было найдено в нач. 20 в. для задачи о лучистом равновесии в звездных атмосферах. Физич. смысл уравнения переноса - баланс энергии, числа квантов, числа частиц в элементе фазового пространства координат и скоростей частиц:

(*)

где Ф (r, v, t )-функция распределения частиц в точке r, v - скорость, t - момент времени, 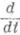- полная производная по траектории движения частицы, - скорость изменения функции распределения за счет столкновения частиц с веществом (нейтронов с ядрами или квантов с атомами вещества), S - мощность источника частиц. Для электромагнитного излучения в качестве независимых переменных функции распределения, определяющей среднюю интенсивность излучения, входят вектор направления излучения и его частота. Одни и те же уравнения для описания распространения частиц и квантов получаются вследствие одинакового физич. смысла этих кинетич. уравнений - баланс энергии в фазовом пространстве. Член, описывающий столкновения, является интегральным:

а само уравнение переноса (кинетическое уравнение) - интегро-дифференциальным уравнением. Здесь S - полное сечение взаимодействия частиц с веществом в элементарном акте столкновения, 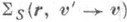- сечение перехода (вероятность перехода) из скорости v' до рассеяния в скорость vпосле рассеяния (с учетом вероятности, что столкновение произойдет). Для свободного движения частиц полная производная от функции распределения по траектории движения имеет вид

Для полного определения решения необходимо задать начальное условие

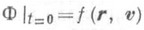
и граничное условие. На границе тела (области пространства, внутри к-рой решается уравнение переноса) могут быть заданы, напр., условия абсолютного поглощения частиц

где п - внешняя нормаль к поверхности (границе) тела. Возможны и более общие граничные условия, описывающие отражение частиц от границы или "прострел" частиц через вакуум (для невыпуклого тела, граничащего с вакуумом - областью, где нет столкновений). Математич. исследование уравнений переноса в односкоростном случае, т. е. в предположении, что изменяется лишь направление распространения излучения или частиц при постоянной энергии кванта или частицы, было проведено B.C. Владимировым [1] для случая =0. При изотропном рассеянии задача сводится к интегральному уравнению с положительным ядром, к к-рому применима теория вполне непрерывных операторов, оставляющих инвариантным конус в банаховом пространстве. При этом однородная задача имеет положительное собственное значение (стоящее множителем при интеграле столкновений), к-рое не больше модуля всякого другого собственного значения l_i, и ему отвечает, по крайней мере, одна неотрицательная собственная функция (соответствующая l₁). Эта теорема обобщается на случай анизотропного рассеяния. В широком классе случаев первое собственное значение задачи оказывается простым, а собственная функция, соответствующая ему,- положительной почти всюду в фазовом пространстве координат и направлений.

Таков, напр., случай, когда 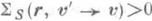почти всюду. Найдены условия, при к-рых для уравнения переноса с анизотропным рассеянием справедлива теория Гильберта - Шмидта, построен новый вариационный функционал для уравнений переноса с четной вероятностью перехода относительно переменной m₀=(v,v'). С помощью нового вариационного метода последовательно исследованы уравнения метода сферич. гармоник, к-рые вместе с краевыми условиями получаются применением прямого вариационного метода Галеркина к уравнению переноса, если в качестве пробных функций взять линейные комбинации сферич. функций, зависящих от направления распространения, умноженных на неизвестные функции пространственных координат. Вариационный принцип позволил отобрать наилучшие граничные условия для метода сферич. гармоник, ранее найденные эмпирически, из вдвое большего количества возможных линейно независимых условий на границе тела (для плоской геометрии) (см. [1]).

В нестационарном случае (см. [2]) при исследовании спектра собственное значение при переходе к интегральному уравнению (для изотропного рассеяния) нелинейно входит в ядро интегрального уравнения. Это обстоятельство приводит в конечном счете к тому, что число точек дискретного спектра оказывается конечным (а в некоторых случаях - нестационарная задача для тепловых нейтронов в малом блоке замедлителя - их вообще нет), кроме того, появляется сплошной спектр собственных значений.

В ряде случаев удается получить аналитическое решение уравнения переноса. Например, методом Винера - Хопфа решается задача Милна; метод разложения по сингулярным собственным функциям оператора переноса позволяет решить ряд одномерных задач [3].

В связи с потребностями инженерной практики были развиты оперативные численные методы решения уравнения переноса нейтронов для расчета критич. режима ядерного реактора (задача на собственные значения для уравнения (*) при ). Одним из основных методов решения является метод сферич. гармоник, к-рый, однако, сложен для реализации на ЭВМ и, как, впрочем, и другие методы, медленно сходится (это объясняется наличием особенности в ядре интегрального уравнения переноса). См. Переноса уравнения;численные методы решения.

Лит.:[1] Владимиров В. С., "Тр. Матем. ин-та АН СССР", 1961, т. 61; [2] Шихов С. В., Вопросы математической теории реакторов. Линейный анализ, М., 1973; [3] Кейз К., Цвайфель П. Ф., Линейная теория переноса, пер. с англ., М., 1972; [4] Соболев В. В., Перенос лучистой энергии в атмосферах звезд и планет, М., 1956. В. А. Чуянов.