ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ

       

физическая теория, рассматривающая пространственно-временные закономерности, справедливые для любых физ. процессов. Универсальность пространственно-временных св-в, рассматриваемых О. т., позволяет говорить о них просто как о .св-вах пространства-времени. Наиболее общая теория пространства-времени наз. общей теорией относительности (ОТО) или теорией тяготения, т. к. согласно этой теории св-ва пространства-времени в данной области определяются действующими в ней полями тяготения. В излагаемой ниже частной теории относительности, основы к-рой были даны А. Эйнштейном в 1905, изучаются св-ва пространства-времени, справедливые с той точностью, с какой можно пренебрегать действием тяготения. Т. о., логически частная О. т. есть частный случай ОТО; исторически построение ОТО было завершено Эйнштейном позже (в 1915), после чего и появился термин «частная О. т.». В рус. литературе последняя наз. также специальной О. <т. (что соответствует букв. переводу нем. слова speziell —.специальный, частный) или просто О. т.

Основные черты О. т. Явления, описываемые О. т., наз. релятивистскими (от лат. relativus — относительный) и проявляются при скоростях движения тел, близких к скорости света в вакууме с=2,99792458(1,2)X 1010 см/с. При таких скоростях (их принято называть релятивистскими) зависимость энергии ? тела от его скорости v описывается уже не ф-лой классич. механики

?кин = mv2/2, а релятив. ф-лой

?=mc2/?(1-v2/с2 ). (1) Масса т, входящая в эту ф-лу, наз. также массой покоя тела. Из (1) видно, что энергия тела стремится к бесконечности при v ®с, поэтому, если m?0, скорость тела всегда меньше с, хотя при ?->mс2 она может стать сколь угодно близкой к ней. Это наблюдается, напр., в опытах на ускорителях заряж. ч-ц, в к-рых ч-цам сообщаются энергии, много большие mc2, и они поэтому движутся со скоростью, практически равной с. Со скоростью света всегда движутся ч-цы, масса покоя к-рых равна нулю (фотоны, возможно, нейтрино). Скорость с явл. предельной скоростью передачи любых вэ-ствий и сигналов из одной точки пр-ва в другую.

Существование предельной скорости означает необходимость глубокого изменения обычных пространственно-временных представлений, основанных на повседневном опыте. Рассмотрим след. мысленный опыт. В вагоне, движущемся со скоростью v относительно полотна железной дороги, посылается световой сигнал в направлении движения. Скорость сигнала для наблюдателя в вагоне равна с. Если бы длины и промежутки времени, измеряемые любым наблюдателем, были одинаковы, то выполнялся бы закон сложения скоростей классич. механики, и для наблюдателя, стоящего у железнодорожного полотна, скорость сигнала была бы равна c+v, т. е. больше предельной. Противоречие устраняется тем, что для наблюдателя, относительно к-рого физ. система движется со скоростью v, все процессы в этой системе замедляются в 1/?(1-v2/c2) раз (это явление наз. замедлением времени), а продольные (вдоль движения) размеры тел во столько же раз сокращаются, и события, одновременные для одного наблюдателя, оказываются неодновременными для другого, движущегося относительно первого (т. н. о т н о с и т е л ь н о с т ь о д н о в р е м е н н о с т и). Учёт этих эффектов приводит к закону сложения скоростей, при к-ром предельная скорость одинакова для всех наблюдателей (см. ниже).

Характерное для О. т. явление замедления времени наблюдается при распадах нестабильных элем. ч-ц косм. лучей или получаемых с помощью ускорителей высоких энергий. Такие ч-цы движутся со скоростями, близкими к с, и, с точки зрения земного наблюдателя, их времена жизни, а следовательно, и проходимые ими от рождения до распада расстояния увеличиваются в тысячи и десятки тысяч раз.

Из релятив. ф-лы для энергии следует, что при малых скоростях (v<- с) энергия . тела равна: ?=mc2+mv2/2. Второй член справа есть обычная кинетич. энергия, первый же член показывает, что покоящееся тело обладает запасом энергии ?0=mc2, наз. э н е р г и е й п о к о я (т. н. принцип эквивалентности энергии и массы, или принцип эквивалентности Эйнштейна). В яд. реакциях и процессах превращений элем. ч-ц значит. часть энергии покоя может переходить в кинетич. энергию ч-ц. Так, источником энергии, излучаемой Солнцем, явл. превращение четырёх протонов в ядро гелия; масса ядра гелия меньше массы четырёх протонов на 5•10-26 г, поэтому при каждом таком превращении выделяется 4,5•10-5 эрг энергии, уносимой излучением. За счёт излучения Солнце теряет в 1 с 4•109кг своей массы.

О. т. подтверждена обширной совокупностью фактов и лежит в основе всех совр. теорий, рассматривающих явления при релятив. скоростях.

Принцип относительности и другие принципы инвариантности. Возникновение частной О. т. В основе О. т. лежит принцип относительности, согласно к-рому в физ. системе, приведённой в состояние свободного равномерного и прямолинейного движения относительно системы, условно наз. «покоящейся», для наблюдателя, движущегося вместе с системой, все процессы происходят в точности так же, как в покоящейся системе. Этот факт формулируют в виде утверждения об инвариантности законов природы относительно преобразований движения. Термин «принцип относительности» связан с тем, что если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел останутся неизменными.

Наряду с принципом относительности из опыта известны и др. принципы инвариантности, или симметрии, законов природы. Любой физ. процесс происходит точно так же,

1) если осуществить его в любой др. точке пр-ва; эта симметрия выражает равноправие всех точек пр-ва, однородность пр-ва;

2) если систему, в к-рой происходит процесс, повернуть на произвольный угол; эта симметрия выражает равноправие всех направлений в пр-ве, изотропию пр-ва; 3) если повторить процесс через нек-рый произвольный промежуток времени; эта симметрия выражает однородность времени.

Т. о., имеет место инвариантность законов природы по отношению к четырём типам преобразований: 1) переносу в пр-ве,

2) вращению в пр-ве,

3) сдвигу во времени,

4) преобразованию движения.

Симметрии 1—4 выполняются точно только в изолированной от внеш. воздействий системе, т. е. если можно пренебречь воздействием на систему внеш. факторов; для реальных систем они справедливы лишь приближённо.

Изучение св-в преобразований 1, 2 составляет предмет евклидовой геометрии трёхмерного пр-ва, если рассматривать её как физ. теорию, описывающую св-ва физ. объектов (при этом под переносом следует понимать преобразование параллельного переноса).

При скоростях тел v, сравнимых с с, обнаруживается тесная связь и матем. аналогия между преобразованиями 1, 3 и 2, 4. Это даёт основание говорить об О. т., в к-рой все преобразования 1—4 следует рассматривать совместно, как о геометрии пространства-времени. Содержанием О. т. явл. рассмотрение св-в преобразований 1—4 и следствий из соответствующих принципов инвариантности. Математически О. т. явл. обобщением геометрии Евклида — геометрией четырёхмерного Минковского пространства-времени.

Принцип относительности был известен (и справедлив) в классич. механике, но св-ва преобразований движения при v<- с и при v = с различны; при v<-с релятив. эффекты исчезают и преобразования движения переходят в преобразования Галилея, справедливые для классич. механики (см. ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ).

Осн. понятие О. т.— точечное событие, т. <е. нечто, происходящее в данной точке пр-ва в данный момент времени (напр., выстрел, распад элем. ч-цы). Это понятие явл. абстракцией — реальные события всегда имеют нек-рую протяжённость в пр-ве и во времени и могут рассматриваться как точечные только приближённо. Любой физ. процесс есть последовательность событий (С): C1, C2, . . ., Сn, . . . Справедливость симметрии 1—4 означает, что наряду с последовательностью (С) законы природы допускают существование бесконечного числа др. последовательностей (С), к-рые получаются из (С) соответствующим преобразованием и различаются положением событий в пр-ве и времени, но имеют одинаковую с (С) внутр. структуру. Напр., в случае симметрии 4 можно наглядно описать процесс (С) как происходящий в стоящем на земле самолёте, а процесс (С) как такой же процесс, происходящий в самолёте, летящем с пост. скоростью (относительно земли); разл. скоростям и направлениям движения соответствуют разл. последовательности (С). Преобразования, переводящие одну последовательность событий в другую, наз. активными (в отличие от п а с с и в н ы х преобразований, к-рые связывают координаты одного и того же события в двух системах координат; см. ниже). Совокупность всех возможных преобразований (1—4) с матем. точки зрения должны составлять группу; она наз. группой Пуанкаре. Преобразования группы Пуанкаре носят универс. хар-р: они действуют одинаково на события любого типа. Это позволяет считать, что они описывают св-ва пространства-времени, а не св-ва конкретных процессов. Преобразования Пуанкаре могут быть описаны разл. способами (так же, как можно описывать разл. способами движения в трёхмерном пр-ве); наиб. простое описание получается при использовании инерциальных систем отсчёта (и. с. о.) и связанных с ними часов. Роль и. с. о. в О. т. такая же, как роль прямоугольных декартовых координат в геометрии Евклида.

Осознание универс. справедливости принципа относительности для любых физ. явлений — результат сложного историч. развития. В 19 в. считалось, что принцип относительности справедлив только в механике, но несправедлив в оптике и в электродинамике, т. к. представлялось очевидным, что эл.-магн. волны (в т. ч. свет) — это волны в особой среде — эфире, заполняющем всё пр-во и определяющем привилегированную систему отсчёта, покоящуюся относительно эфира, в к-рой только и справедливы законы оптики и ур-ния электродинамики. Казалось очевидным, что в системе тел, движущейся относительно эфира, оптич. и эл.-магн. явления будут происходить иначе, чем в неподвижной, но все попытки обнаружить явление такого рода, предпринимавшиеся в 19 в. и в нач. 20 в., потерпели неудачу. Объяснение неудач искали, начиная с франц. физика О. Ж. Френеля, в динамике: используя конкретные динамич. законы, сформулированные в системе покоя эфира, показывали, что в данной системе тел эффекты, связанные с движением относительно эфира, компенсируются. Эта программа нашла известное завершение в работах голл. физика X. Лоренца и франц. математика А. Пуанкаре (1904—05), где было показано, что если принять лоренцовский вариант электродинамики эл-нов и предложенную Пуанкаре модель :эл-на, сжимаемого пост. давлением эфира, то компенсация будет точной и принцип относительности, понимаемый как невозможность обнаружения движения относительно эфира, выполняется. В 1905 в работе Пуанкаре были исследованы групповые св-ва преобразований движения и преобразований вращения с точки зрения наблюдателя, покоящегося относительно эфира. Переход к совр. точке зрения, согласно к-рой в абсолютно пустом пр-ве нельзя определить покоящуюся систему отсчёта и все связанные преобразованиями движения и . с. о. равноправны, был сделан Эйнштейном в 1905. В его работе была развита последоват. теория измерений времени и координат в и. с. о. и обнаружен относит. хар-р релятив. замедления времени и сокращения масштабов. Матем. аппарат теории в полной форме был развит нем. учёным Г. Минковским в 1908.

Инерциальные системы отсчёта. С той степенью точности, с какой св-ва данной области пространства-времени описываются частной О. т., можно ввести и. с. о., в к-рых описание пространственно-временных закономерностей О. т. принимает особенно простую форму. Под системой отсчёта в этом случае можно подразумевать жёсткую систему тв. тел (или её мысленное продолжение), по отношению к к-рой определяются положения событий, траектории тел и световых лучей. Любая система отсчета, движущаяся относительно данной и. с. о. равномерно и прямолинейно, без вращения, также будет инерциальной, а система отсчёта, вращающаяся или движущаяся ускоренно, уже не будет и. с. о. Таким образом, и. с. о. образуют выделенный класс систем отсчёта. В и. с. о. справедлив закон инерции, т. е. свободная ч-ца движется в и. с. о. прямолинейно и (при принятой синхронизации часов, см. ниже) равномерно. Требование выполнения закона инерции может быть принято как определение и. с. о. Первый закон Ньютона может рассматриваться при этом как утверждение о существовании таких систем отсчёта. Все и. с. о. равноправны, это равноправие явл. непосредств. выражением принципа относительности.

В области пространства-времени, в к-рой справедлива частная О. т., можно пользоваться и неинерц. системами отсчёта (так же, как можно пользоваться криволинейными координатами в геометрии Евклида), но при этом описание св-в пространства-времени оказывается более сложным.

В данной и. с. о. необходимо определить способ измерения времени и координат. В и. с. о. трёхмерная пространств. геометрия — евклидова, если прямые определить, напр., как траектории световых лучей, а расстояния измерять тв. масштабами. Поэтому в данной и. с. о. можно ввести декартовы прямоуг. координаты х, у, z. Для определения времени t события удобно представить, что в той точке, где оно произошло, находятся часы, покоящиеся в данной и. с. о. Если события происходят в разных точках А, В, то для сравнения их времён нужно синхронизировать часы в А и В, т. е. определить, что означает, что часы в А и В показывают одинаковое время. Обычное определение таково: пусть в момент tА по часам из А посылается сигнал в В, а в момент его прибытия в В посылается такой же сигнал из В в А ', если сигнал пришёл в Л в момент t'А , то принимается, что сигнал пришёл в 5 в момент tB=(tA+t'A)/2, и соотв. устанавливаются часы в В. При таком определении времена распространения сигнала из А в В и из В в А одинаковы и равны (T'А-TA)/2. Сигналами могут служить световые вспышки, звук. сигналы (если среда, в к-рой они распространяются, покоится по отношению к данной системе отсчёта), выстрелы из двух одинаковых орудий, установленных в А и В, и т. д., требуется лишь, чтобы условия передачи сигнала из А в A в и из В в А были одинаковыми. Целесообразность такого определения времени связана с тем, что в любой и. с. о. отсутствует к.-л. физически выделенное направление; описанная процедура синхронизации часов симметрична относительно А и В и поэтому не вносит анизотропии в способ описания. Отсутствие выделенного направления проявляется в том, что синхронизация любыми сигналами приводит к одному и тому же результату; к такому же результату приводит медленный (с v<-с) перенос часов из А в В. При практич. измерениях времён и координат используются многочисленные косвенные методы при условии, что они дают тот же результат, что и описанные выше процедуры. В любой другой и. с. о. координаты и время измеряются с помощью таких же масштабов и часов, синхронизируемых таким же способом. Заранее не очевидно, что времена, определённые таким методом в двух разл. и. с. о., будут одними и теми же, и они действительно оказываются различными. После того как синхронизация произведена, могут измеряться скорости ч-ц и сигналов в данной и. с. о., в частности скорость распространения световых сигналов. Скорость света в любой и. с. о. всегда равна с.

Преобразования Лоренца. Рассмотренные активные преобразования непосредственно связаны с пассивными преобразованиями, описывающими связь между координатами и временем данного события в двух разл. и. с. о. В силу принципа относительности безразлично, сообщить ли телу скорость V по отношению к данной и. с. о. L или перейти к системе отсчёта L', движущейся со скоростью V относительно L,— закон преобразования координат и времени должен быть одним и тем же.

В силу справедливости симметрии 1—4 преобразования, связывающие координаты и времена события х, у, z, t и x', у', z', t', измеренные в двух и. с. о. L и L', должны быть линейными. Из симметрии 1—4 и требования, чтобы преобразования составляли группу, можно получить вид этих преобразований. Если система отсчёта L' движется относительно L со скоростью V, то при надлежащем выборе осей координат и начал отсчёта времени в L и L' (оси х и х' направлены по V, оси у и y', z и z' соотв. параллельны, начала координат О и О' совпадают при t=0 и часы в L' установлены так, что при t=0 часы в О' показывают время t'=0) преобразования координат и времени имеют вид: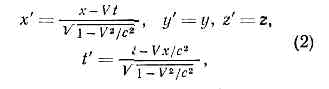

где с — параметр преобразования, имеющий смысл предельной скорости движения (равной скорости света в вакууме). Этот параметр может быть определён из любого эффекта О. т. (напр., из замедления времени распада быстрого p-мезона). Справедливость кинематики и динамики, основанных на преобразованиях (2), подтверждена неисчислимой совокупностью эксперим. фактов.

Преобразования Лоренца (2) вместе с преобразованиями вращения вокруг начала координат образуют г р у п п у Л о р е н ц а; добавление к ней сдвигов во времени t' =t+a и в пр-ве х'=х+b (где a, b — произвольные постоянные размерности времени и длины) даёт группу Пуанкаре.

Т. к. законы природы должны иметь одинаковую форму во всех и. с. о., они должны сохранять свой вид при преобразованиях Лоренца. Это требование наз. принципом (постулатом) р е л я т и в и с т с к о й и н в а р и а н т н о с т и, или л о р е н ц-и н в а р и а н т н о с т и (лоренц-ковариантности), законов природы.

Из преобразований Лоренца вытекает релятив. закон сложения скоростей. Если ч-ца или сигнал движется в L по оси х со скоростью v, то в момент t x=vt и в системе L' скорость ч-цы v' = x'lt' равна:

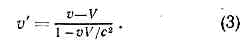Из этой ф-лы видна осн. черта релятив. кинематики — независимость скорости света от движения источника. Действительно, если скорость света, испущенного покоящимся в нек-рой и. с. о. L источником, есть с, v=c, то из (3) получим, что в и. с. о. L' скорость света v' также равна с. Т. к. направление оси произвольно, то отсюда следует независимость скорости света от движения источника. Это св-во скорости света однозначно определяет вид преобразований Лоренца: постулировав независимость скорости света от движения источника, однородность пр-ва и времени и изотропию пр-ва, можно вывести преобразования Лоренца.

Из преобразований Лоренца легко получить осн. эффекты О. т.: относительность одновременности, замедление времени, сокращение продольных размеров движущихся тел. Действительно, события 1, 2, одновременные в одной и. с. о. L, t1=t2, оказываются неодновременными в другой и. с. о. L', t'2-t'1=(x1-x2)V!c2?(1-V2/c2)?0. Далее, когда часы, покоящиеся в L в точке x=0, показывают время t, то время t' по часам в L', пространственно совпадающим с часами в L в этот момент времени, есть

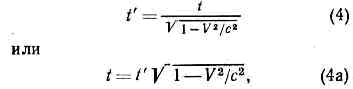т. е., с точки зрения наблюдателя в L', часы в L отстают. В силу принципа относительности, с точки зрения наблюдателя в L', все процессы в L замедлены в такое же число раз.

Легко получить также, что размеры l всех тел, покоящихся в L, оказываются при измерении в L' сокращёнными в 1/?(1-V2/c2)раз в направлении V:

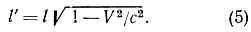В частности, продольный диаметр сферы, движущейся со скоростью v относительно L, при измерении в L' будет в 1/?(1-v2/c2) раз короче, чем поперечный. (Заметим, что это сокращение не обнаружилось бы на мгновенной фотографии сферы: из-за разл. запаздывания световых сигналов, приходящих от разных точек сферы, её видимая форма остаётся прежней.)

Для и. с. о. пространственно-временные эффекты, определяемые преобразованиями Лоренца, относительны: с точки зрения наблюдателя в L, замедляются все процессы и сокращаются все продольные масштабы в L'. .Однако это утверждение несправедливо, если хотя бы одна из систем отсчёта неинерциальна. Если, напр., часы 1 перемещаются относительно L из А в В со скоростью v, а потом из В в А со скоростью -v, то часы 1 отстанут по сравнению с часами 2, покоящимися в A, в 1/?(1-v2/c2) раз; это можно обнаружить прямым сравнением, так что эффект абсолютен. Он должен иметь место для любого процесса; напр., близнец, совершивший путешествие со скоростью v, вернётся в 1/?(1-v2/с2) раз более молодым, чем его брат, остававшийся неподвижным в и. с. о. Это явление, получившее назв. парадокса близнецов, в действительности не содержит парадокса: система отсчёта, связанная с часами 1, не явл. инерциальной, т. е. эти часы испытывают ускорение при повороте в В по отношению к инерц. системе; поэтому часы 1 и 2 н е р а в н о п р а в н ы.

При малых скоростях v преобразования Лоренца переходят в преобразования Галилея х'=х-vt, y'=y, z' = z, t'=t, к-рые описывают связь между картинами разл. наблюдателей, известную из повседневного опыта: размеры предметов и длительность процессов одинаковы для всех наблюдателей.

Преобразования Пуанкаре оставляют инвариантной величину, наз. интервалом sAB между событиями А и В, к-рый определяется соотношением:

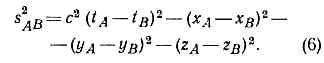Математически инвариантность s аналогична инвариантности расстояния при преобразованиях движения в евклидовой геометрии. Величины ct, x, у, z можно рассматривать как четыре координаты события в четырёхмерном пространстве-времени Минковского: x0=ct. xl=x, x2=y, x3=z,

к-рые явл. компонентами четырёхмерного вектора.

С матем. точки зрения частная О. т. есть геометрия пространства-времени Минковского. (Если вместо х0 ввести мнимую координату x4=ix0=ict, то произвольное преобразование Пуанкаре можно записать в виде, полностью аналогичном ф-ле, описывающей вращения и сдвиги в трёхмерном пр-ве.) Вследствие того, что квадраты разностей временных и пространств. координат входят в (6) с разными знаками, знак s2 может быть различным, геометрия такого пр-ва отличается от евклидовой и наз. п с е в д о е в к л и д о в о й.

Законы сохранения в О. т. и релятивистская механика. В О. т., так же как в классич. механике, для замкнутой физ. системы сохраняется импульс р и энергия ?. Трёхмерный вектор импульса вместе с энергией образует четырёхмерный вектор энергии-импульса с компонентами ?/с, р. При преобразованиях Лоренца остаётся инвариантной величина

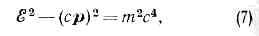где т — масса покоя ч-цы. Из требований лоренц-инвариантиости следует, что зависимость энергии и импульса от скорости имеет вид:

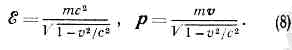Энергия и импульс ч-цы связаны соотношением p=?v/c2. Оно справедливо также для ч-цы с нулевой массой покоя; тогда v=c и р=?/с.

Обсуждалась возможность существования объектов, движущихся со скоростью, большей скорости света в вакууме (т. н. тахионов). Формально это не противоречит лоренц-пнварнантности, но приводит к серьёзный затруднениям с выполнением принципа причинности.

Масса покоя т не явл. сохраняющейся величиной. В частности, в процессах распадов и превращений элем. ч-ц сумма энергий и импульсов ч-ц сохраняется, а сумма масс покоя меняется. Так, в процессе аннигиляции позитрона и эл-на в два фотона, е++е-®2g, сумма масс покоя изменяется на 2mе (mе — масса покоя эл-на).

В системе отсчёта, в к-рой тело покоится (такая система отсчёта наз. с о б с т в е н н о й), его энергия (энергия покоя) есть ?0=mс2. Если тело, оставаясь в покое, изменяет своё состояние, получая энергию в виде излучения или тепла, то из релятив. закона сохранения энергии следует, что полученная телом энергия D? связана с увеличением его массы покоя соотношением D?=Dmс2. Величина ?0=mс2 определяет макс. величину энергии, к-рая может быть «извлечена» из данного тела в системе отсчёта, в к-рой оно покоится.

Для движущегося тела величина

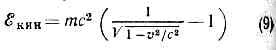определяет его кинетич. энергию. При v<-с (9) переходит в нерелятив. выражение ?кин=mv2/2, при этом импульс p=mv. Из определения ?кин следует, что для любого процесса в изолированной системе выполняется равенство:

D(S?кин) = -с2D(Sm). (10)

согласно к-рому увеличение кинетич. энергии пропорц. уменьшению суммы масс покоя. Это соотношение широко используется в яд. физике; оно позволяет предсказывать энерговыделение в яд. реакциях, если известны массы покоя участвующих в них ч-ц. Возможность протекания процессов, в к-рых происходит превращение энергии покоя в кинетич. энергию ч-ц, ограничена др. законами сохранения (напр., законом сохранения барионного заряда, запрещающим процесс превращения протона в позитрон и g-квант). Иногда вводят массу, определяемую как

mдвиж=m/?(1-v2/c2) (11)

При этом связь между импульсом и скоростью приобретает тот же вид, что и в ньютоновской механике: р=mдвижv. Так определ. масса отличается от энергии тела лишь множителем 1/с2. (В теор. физике часто выбирают ед. измерения, полагая с=1, тогда ?=m.)

Осн. ур-ния релятив. механики имеют такой же вид, как и второй закон Ньютона и ур-ние энергии, только вместо нерелятив. выражений для энергии и импульса используются выражения (8):

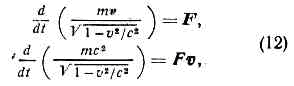где F — сила, действующая на тело. Для заряж. ч-цы, движущейся в эл.-магн. поле, F есть Лоренца, сила.

О. т. и эксперимент. Предположения о точечных событиях (означающее локальность вз-ствий), о справедливости принципа относительности, однородности времени и однородности и изотропии пр-ва с неизбежностью приводят к О. т. При этом абстрактно допустим предельный случай, соответствующий с=?, однако такая возможность исключается экспериментом: доказано, что предельная скорость с есть скорость света в вакууме.

Каковы границы применимости О. т.? Отклонения от пространственно-временной геометрии О. т., связанные с гравитацией, наблюдаемы и рассчитываются в ОТО; никаких других ограничений применимости О. т. не обнаружено, хотя неоднократно высказывались предположения, что на очень малых расстояниях (напр., =10-17 см) понятие точечного события, а следовательно, и О. т. могут оказаться неприменимыми (см. КВАНТОВАНИЕ ПРОСТРАНСТВА-ВРЕМЕНИ). Совр. квант. теории фундам. вз-ствий (эл.-магн., слабого, сильного) целиком основаны на геометрии пространства-времени частной О. т. Из этих теорий с наиб. высокой точностью проверена квант. электродинамика лептонов, применимость к-рой установлена до расстояний 10-16 см. Отсюда следует, что по крайней мере до этих расстояний действует геометрия частной О. т. Неоднократно повторялись с высокой точностью классич. опыты, использовавшиеся для обоснования О. т. в первые десятилетия её существования (Майкельсона опыт и др.). Такого рода опыты сейчас представляют в основном историч. интерес, т. к. осн. массив подтверждений ОТО составляют данные, относящиеся к вз-ствиям релятив. элем. ч-ц, где справедливость кинематики частной О. т. проверена на обширном материале.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ

Содержание:

Введение
Группа Пуанкаре
Группа Лоренца
Аберрация света и видимая форма предметовв частной О. т.
Пространство скоростей
Векторы и тензоры в пространстве Минковского498 Спинорные представления группы Лоренца
Структура пространства Мнаковского
Релятивистская механика
Экспериментальные основания частной О. <т.

О. т. - теория, описывающая универс. пространственно-временныесвойства физ. процессов. Поскольку эти свойства справедливы для всех известныхв физике процессов и взаимодействий, об О. т. говорят просто как о физ. <теории пространства-времени.

Введение

Возникновение О. т. связано с неудаченобнаружить движение Земли относительно эфира.X. А. Лоренц (Н. A.Lorentz) и А. Пуанкаре (Н. Poincare) в 1904 - 05 смогли объяснить невозможностьобнаружения этого движения, оставаясь в рамках представления о выделенностисистемы координат, в к-рой эфир покоится. Совр. точка зрения, основаннаяна принципе относительности Эйнштейна, была сформулирована А. Эйнштейном(A. Einstein) в 1905; при этом было исключено понятие механич. эфира. Большойвклад в развитие матем. аппарата теории внёс в 1908 - 10 Г. Минковский(Н. Minkowski), к-рому принадлежит и интерпретация О. т. как геометриичетырёхмерного пространства-времени [1 - 4].
После появления теории тяготения Эйнштейна, <построение к-рой было начато Эйнштейном в 1907 и завершено X. Д. Гильбертом(Н. О. Hilbert) и Эйнштейном в 1915 (первое обобщающее изложение теориибыло дано Эйнштейном в 1916), и её эксперим. подтверждения стало ясно, <что свойства пространства-времени в данной области зависят от действующихв ней гравитац. полей (см. Тяготение). В О. т. рассматривается частныйслучай - свойства пространства-времени в областях, где полями тяготенияможно с желаемой точностью пренебречь; отсюда термин - частная, или специальная, <О. т. (последний термин возник в результате неудачного букв. перевода нем. <слова speziell - частный). Осн. понятие О. т. - событие, под к-рым понимаетсянечто происходящее в данный момент времени в данной точке пространства(напр., вспышка света или совпадение стрелки прибора с делением шкалы).Реальные события имеют конечную протяжённость в пространстве и времени, <поэтому понятие события в О. т. является идеализацией. Опыт показывает, <что применимость этой идеализации очень высока, вплоть до расстояний ~10^-16 см и времён ~10^-26 с.
Предполагается, что потенц. совокупностьсобытий образует четырёхмерный континуум. Каждое событие может быть охарактеризованотройкой действит. чисел, определяющей его пространств. положение, и ещёодним действит. числом, определяющим момент времени, в к-рый это событиепроисходит. Предполагается, что пространство-время непрерывно, т. е. любойтакой четвёрке чисел в нек-рой области числового пространства может бытьпоставлено в соответствие нек-рое событие и близким событиям отвечают близкиечетвёрки чисел.
Области пространства-времени, где справедливачастная О. т., характеризуются тем, что в них могут быть введены локально инерциальные системы отсчёта (и. с. о.), в к-рых свободные от внеш. <воздействий точечные тела и импульсы света движутся прямолинейно и равномерно. <В реальной Вселенной гравитац. поля глобально не устранимы и присутствуютвсюду. При наличии таких полей условия, требуемые для введения и. с. о.,не выполняются, в частности ни точечные тела, ни импульсы света не движутсяпрямолинейно. Однако в тех областях, где эти поля однородны, можно, в силу эквивалентности принципа, ввести падающие свободно и без вращениясистемы отсчёта, в к-рых эти поля исчезают. Такие системы отсчёта и являютсяинерциальными. Любая система отсчёта, движущаяся равномерно и без вращенияотносительно данной и. с. о., также является инерциальной. В и. с. о. справедливаевклидова геометрия для пространства. Утверждение о равномерности движенияпредполагает определённый выбор синхронизации часов в разных точках и. <с. о. (см. ниже).
Пример и. с. о. - система отсчёта, связаннаяс искусств. спутником Земли, стабилизированным относительно вращения спомощью гироскопа. В такой системе отсчёта не действуют ни гравитац. полеЗемли, ни поля Солнца и Галактики в той степени, в какой эти поля однородныв масштабе спутника. Если рассматривать систему отсчёта, связанную с Землёй, <то она уже не будет инерциальной как из-за вращения Земли, так и из-запоявления в ней собств. гравитац. поля Земли. Однако на расстояниях, большихпо сравнению с размерами области, где гравитац. поле Земли велико, но малыхпо сравнению с расстоянием до Солнца, систему отсчёта, связанную с Землёй, <можно считать инерциальной, т. к. Земля свободно падает в гравитац. полеСолнца.
Практически вопрос о том, можно ли даннуюсистему отсчёта считать инерциальной, зависит от характера производимогоопыта и требуемой точности. Так, при выполнении большинства оптич. опытовсистема, связанная с Землёй, может считаться инерциальной даже на поверхностиЗемли; то же относится к экспериментам в физике элементарных частиц. Сдр. стороны, камень, брошенный вблизи Земли, не движется прямолинейно иравномерно, и для него эта система отсчёта не инерциальна. Характернымпараметром, определяющим возможность введения и. с. 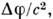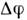о., является отношение где - изменениегравитац. потенциала в рассматриваемой области. Напр., при измерении Доплераэффекта 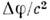в области измерения должно быть мало по сравнению с величиной v/c, где v - скорость источника, с - скорость света.
В области, где справедлива частная О. <т., можно ввести и неиперц. системы отсчёта, в к-рых свойства пространства-временинужно описывать с помощью аппарата общей теории относительности. В этомслучае условие применимости частной О. т. имеет вид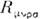 = 0, где 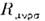- тензор Римана ( кривизны тензор), или более точно 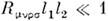,где l₁, l₂ - характерные для данногоопыта длины. При условии 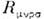= 0 всегда можно ввести совокупность и. с. о. Если условие 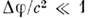при линейном законе изменения 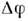характеризует неинерциальность, к-рая может быть устранена переходом вдр. систему отсчёта, то мера отклонения 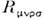от нуля определяет, насколько пространство-время в данной области искривленонеустранимым образом.
Обычно под частной О. т. подразумеваютописание явлений с помощью и. с. о. После того как и. с. о. выбрана, необходимозадать метод определения в ней времён и координат событий. Т. к. в инерц. <системах в частной О. т. справедлива евклидова геометрия, то для определениякоординат событий можно пользоваться декартовыми координатами х¹,х², х³, или х, у,z, где х, у, zизмеряются стандартным жёстким масштабом в ортогональнойдекартовой системе координат. Три координаты х, у, z объединяютсяв трёхмерный вектор r (или х). Время t в данной точке r измеряют любым механизмом, совершающим периодич. движение, т. <е. периодически возвращающимся в данную конфигурацию. Тогда число периодови есть время t. Предполагается, что часы во всех точках пространстваи во всех и. с. о. одинаковы. В совр. метрологии осн. единицы для измерениядлины и времени выбираются с помощью оптич. явлений (число световых волнстандартного излучателя и число атомных колебаний стандартного атома длязаданных переходов).
Для полного задания системы отсчёта необходимоопределить метод сравнения времён событий, происходящих в разных местах. <Опыт показывает, что в и. с. о. пространство изотропно; никаким опытомнельзя выделить физически предпочтительное направление. Естественно выбратьтакую синхронизацию часов, находящихся в разных точках A, В, чтобы не нарушалась эта изотропия. Стандартное определение в частнойО. т. таково. Пусть в момент t₁ из точки . в точку В посылается сигнал (световой импульс, акустич. импульсв среде, находящейся в данной и. с. о., выстрел и т. д.). После прибытиясигнала в В идентичный сигнал посылается из В в А,где принимается в момент времени t₂. Тогда, по определению, <время прибытия сигнала в В есть t = (t_l +t₂)/2; иначе говоря, предполагается, что времена распространениясигнала из А в В и из В в А одинаковы. Двасобытия считаются одновременными (синхронными) в данной и. с. о., есливремена t для них совпадают. Приведённые определения задают в даннойи. с. о. L пространственно-временную координату х, у, z,t. Хотя в действительности область, охватываемая данной и. с. о. L,конечна, удобно допустить идеализиров. ситуацию и предполагать, что всеперечисл. переменные меняются от -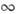до +.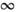
Теоретически можно допустить Вселенную, <в к-рой массы и поля тяготения занимают малую область, а в осп. пространстведействует частная О. т., однако в реальной Вселенной эта возможность нереализована.

Группа Пуанкаре

В области применимости частной О. т. пространство-времяобладает высокой степенью симметрии: все физ. явления инвариантны относительнособств. преобразований Пуанкаре, оставляющих инвариантной метрику пространства-времени Минковского. Последняя определяется квадратом интервала s²,к-рый для двух событий с координатами х ₁, y_l,z_l, t₁ и х ₂, y₂,z₂, t₂ имеет вид:

s² = c²(t₁- t₂)² - (x₁ - x₂)²- (y₁ - y₂)² - (z₁- s₂)². (1)

Пространство-время с такой метрикой наз. Минковского пространством-временем.
Обычно используется сокращённая запись:вводятся четырёхмерный вектор х с компонентами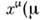 = 0, 1, 2, 3): x⁰ = ct, х ¹= х,x² = y, x³ = z, метрический тензор 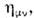к-рый диагоналей и имеет компоненты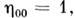 [или 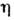= diag (1, - 1, - 1, - 1)], и эйнштейновское правило суммирования, согласнок-рому по совпадающим верхнему и нижнему индексам всегда предполагаетсясуммирование (по греч. индексам суммирование проводится от 0 до 3). В такойзаписи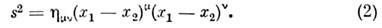

Если рассматриваются преобразования Пуанкаре, <при к-рых любое событие А с координатами x, y, z,t переходит в событие В с координатами 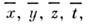то такие преобразования наз. активными.
Собств. преобразования Пуанкаре определяютсякак линейные преобразования вида

непрерывно связанные с тождественным (единичным)преобразованием. Здесь 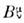- матрица размерности 4 x 4,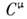- произвольный 4-вектор. Из инвариантности s² относительнопреобразований (3) следует

и 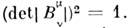Из условия непрерывной связи с единичным преобразованием 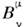= 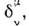где 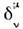- Кронекера символ 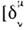=diag (1, 1, 1, 1)], следует, что

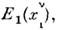
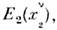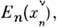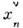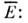
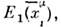
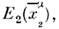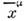Инвариантность законов физики относительнопреобразований Пуанкаре означает, что если возможна последовательностьсобытий Е:...,..., где - 4-координаты n -го события, то возможна и последовательность ...,..., где и 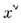связаныпреобразованием (3). Др. словами, законы физики таковы: если последовательность Е допустима и описывает нек-рый физ. процесс, то это же справедливои для последовательности 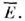Подчеркнём, что координаты 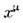и 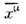измеряютсяв одной и той же системе отсчёта; последовательности Е и 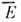- это две разные последовательности событий, связанные активными преобразованиями, <но в то же время по своей внутр. структуре они неразличимы. Это, в частности, <означает, что если два события Е _п, Е_k совпадают, <то совпадают и события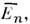 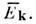Ситуацияаналогична ситуации в геометрии Евклида, где группа активных преобразованийпространства переводит тело из одного положения в другое, не изменяя еговнутр. структуры.
Подвергнем теперь преобразованию Пуанкаресаму систему L, к-рая перейдёт в систему L' с такими же, <как в L, часами и масштабами. Т. к. измерение есть нек-рое событие, <соответствующее фиксации совпадений отсчёта часов и делений на линейкахс нек-рым событием в L, то условие сохранения совпадений означает, <что 4-координаты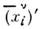 события 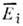в L' и 4-координаты 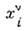события Е _i в L совпадают: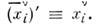
Если ввести преобразование, связывающеекоординаты события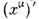 в L' и координаты того же события в L - 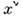(такие преобразования наз. пассивными), то оно будет иметь вид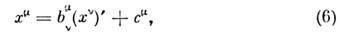

где свойства 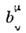и 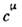такиеже, как и для активного преобразования.
Преобразования Пуанкаре ( Р )образуют группу. Как известно, условия того, что нек-рая совокупность элементовобразует группу, следующие, а) Для любых двух элементов Р₁ и Р₂ определено произведение P₁P₂.В случае преобразований Пуанкаре (активных) произведение определяется какрезультат последоват. выполнения преобразования Р₂ изатем Р₁. Из условия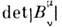 = 1 следует разрешимость (3) относительно 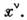б) Операция умножения ассоциативна: Р₁( Р₂ Р₃)= ( Р₁ Р₂) Р₃. Для преобразованийПуанкаре ассоциативность очевидна, т. к. если Р₃ переводитобъект А в B, Р₂ - В в С и P₁ - С в D, то, по определению, ( Р₂ Р₃ )переводит А в С и Р ₁ - С в D; соответственно Р₁( Р₂ Р₃) - А в D. Аналогично ( Р₁ Р₂) - В в D и ( Р ₁ Р ₂ )Р ₃ такжепереводит А в D. в) Существует единица группы I такая, <что IP=PI=Р. Это выполняется, если 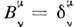, 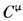= 0.г) Для любого Р существует обратное преобразование Р^-1 такое, что РР^-1 = Р ^-1 Р = I. Последнееочевидно, т. к. вследствие того, что 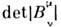= 1, соотношение (3) может быть разрешено относительно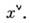
Группа Пуанкаре содержит в качестве подгруппыгруппу сдвигов во времени и в пространстве. Физически это означает, чтов любой и. с. о. опыт, проведённый в др. время или в др. месте, даёт тотже результат (если установка изолирована от внеш. воздействий). Из группыПуанкаре можно выделить подгруппу трёхмерных вращений и сдвигов: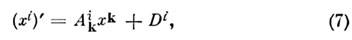

где лат. буквами (i, k =1,2,3) обозначены пространств. индексы. Инвариантность относительно преобразований(7) означает, что в любой и. с. о. пространство однородно и изотропно.
Преобразования (3) содержат также преобразования, <наз. бустами. При таких преобразованиях покоящаяся в L точка ( х'=const) переходит в точку, движущуюся со скоростью v, а точка, <движущаяся в L со скоростью v', переходит в точку, движущуюсясо скоростью v", соответствующей релятивистскому закону сложенияскоростей (см. ниже). В отличие от подгруппы (7), бусты подгруппы не образуют. <Группа Пуанкаре содержит 10 независимых параметров. Коэф.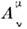или 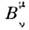с учётомусловия (4) содержит шесть независимых параметров, а четыре сдвига произвольны.
Инвариантность s² относительнопреобразований группы Пуанкаре означает, в частности, инвариантность ур-ния s² = 0. В свою очередь это означает инвариантность скоростисвета относительно всех преобразований, перечисленных выше (в действительности, <согласно частной О. т., со скоростью света движется любая безмассовая частица).В частности, скорость света не изменяется при движении источника. (Событием Е может служить испускание света движущимся источником.) Этот фактявляется одной из основных черт О. т.
Возможность реализации в L и L' последовательностей событий с одинаковыми координатами относительноэтих и. с. о. наз. принципом относительности Эйнштейна. Он означает, чтозаконы природы должны иметь одинаковый вид во всех и. с. о. Для наблюдателейв L и L' соответственно процессы Е и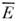 выглядят совершенно одинаково, это наиб. наглядно отражает утверждениео тождественности их внутр. структуры. Если не требовать выполнения условиянепрерывного перехода от матриц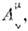 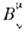к единичной I, то наряду с перечисленными выше преобразованиями, <приводящими к принципу относительности Эйнштейна, появятся также дискретные, <или несобственные, преобразования t- t (обращение времени )и r- r (пространственная инверсия). Инвариантность относительно этихпреобразований в природе нарушается слабым взаимодействием. Не соединяетсянепрерывно с I также преобразование Инвариантность относительно такого преобразования имеет место, если дополнитьего заменой всех частиц на античастицы. Это является общим следствиемквантовой теории поля ( теорема-СРТ).

Группа Лоренца

Группой Лоренца (в математике её наз. собственнойгруппой Лоренца) наз. подгруппа группы Пуанкаре, образуемая преобразованиями(в случае пассивных преобразований) вида

по-прежнему сохраняющая s² и с матрицей 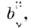непрерывно связанной с единичной матрицей I. Т. к. пространствоМинковского, образуемое точками 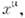однородно, то выделение начала координат в (8) не является ограничением. <Общий случай выбора преобразования (8) соответствует переходу к системеотсчёта, движущейся с пост. скоростью v и с осями, повёрнутыми произвольнымобразом. Очевидно, что он может быть сведён к след. последовательностипреобразований: 1) такому повороту исходной системы осей, чтобы ось х ¹= х совпадала с направлением v; 2) переходу к системеотсчёта с осями х'. y', z', параллельными осям x, у, z системы L, движущейся со скоростью v;3) произвольному повороту осей x, y, z. Число параметровпреобразования равно при этом 6; это совпадает с тем, что матрица 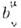удовлетворяет условию 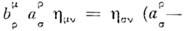матрица 4 x 4, det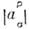=1). Преобразования к параллельным осям, движущимся с произвольной скоростьюо, являющиеся пассивным аналогом бустов, не образуют подгруппы Лоренца, <но преобразования относительно фиксиров. направления движения образуют. <Выберем в качестве направления движения ось x¹. В этомслучае координаты х², x³ не преобразуются:(x²)' = x², (x³)'= х ³. Выберем в (1) в качестве точки 1 начало координат. <Тогда условие инвариантности интервала будет иметь вид

s² = (x⁰)²- (x¹)² - (x²)²- (x ^З)² = (s')²

и s² инвариантен относительно(8). В случае движения по оси х ¹ условие инвариантностисводится к требованию инвариантности выражения ( х ⁰)²- (х ¹)² с очевидным решением:

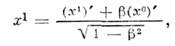
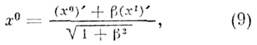
где 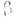=v/c, и соответственно обратным преобразованием: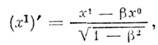

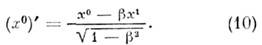
Множитель 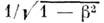имеет стандартное обозначение 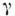(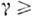1). С точкизрения инвариантности s²,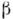может быть произвольным параметром, -1 < b< 1. При 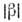= 1 возникает сингулярность, а затем преобразование становится мнимым, <что является одним из выражений недопустимости в частной О. т. скоростей, <больших скорости света.
Полагая в (10) ( х ¹)'=0 (начало координат), имеем х ¹- (v/c)x⁰=0, т. е. (т. к. х ⁰ = ct) v есть скорость движения L' относительно L.

Из ф-л (9) и (10) вытекают два осн. классич. <следствия частной О. т. При измерении в L длины стержня l, покоящегося в L', естественно считать его длиной в L разностькоординат концов, измеренных в одно и то же время в L. Тогда (пользуясьобозначениями х, у, z для координат) имеем для точек А, В стержня

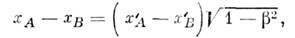
или

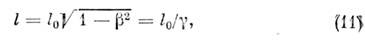
где 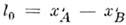(по определению) - длина покоящегося в L стержня, наз. его собственнойдлиной. Т. о., движущийся вдоль своей длины отрезок сокращается в 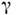раз;это сокращение наз. сокращением Лоренца - Фитцджеральда. Соответственново столько же раз сокращаются все продольные (вдоль движения) размеры движущегосятела. Подчеркнём, что речь идёт именно об определённой процедуре измеренийи вопрос о видимой форме тела в частной О. т. нуждается в отд. рассмотрении. <Для равномерных прямолинейных движений эффект сокращения относителен; наблюдательв L' измерит при аналогичной ситуации сокращение масштаба в L. Однако это несправедливо для непрямолинейного движения. Представимсебе очень большое число стержней, уложенных кольцом внутри обода длины 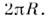Тогда при l₀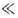R. число стержней, к-рые могут быть уложены по ободу, равно 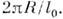Если же стержни быстро скользят вдоль обода, то сокращение Лоренца - Фитцджеральдаприведёт к тому, что окажется возможным уложить 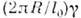стержней. Т. о., сокращение Лоренца - Фитцджеральда есть нек-рое объективноесвойство геометрии пространства-времени Минковского (т. е. свойство пространства 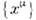,описываемое группой Пуанкаре).
Рассматривая часы, помещённые в L' в начале координат, получаем

т. е. движущиеся часы с точки зрения наблюдателяв L отстают. Так же как и для длин, эффект симметричен: для наблюдателяв L' отстают часы в L. Симметрия связана с характером постановкиопыта; одни движущиеся часы сравниваются с покоящейся синхронизиров. цепочкойчасов в др. системе отсчёта. В случае, если часы движутся по замкнутойтраектории, эффект становится абсолютным. Если часы движутся в течениевремени Т из А в В, апотом обратно из . в А с той же скоростью, то с той точностью, с к-рой можно пренебречьвременем поворота и действием ускорения (а это всегда возможно, если . достаточно велико по сравнению с временем поворота), по часам наблюдателяв А пройдёт 2 Т единиц времени, а по двигавшимся часам 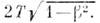Этот эффект, часто называемый парадоксом близнецов, абсолютен. В действительностиникакого парадокса нет, поскольку система отсчёта, связанная с часами, <перестаёт быть инерциальной во время поворота.
Из инвариантности интервала следует, чтов общем случае движущиеся часы, проходящие за время dt расстояние dl, покажут величину интервала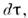 поскольку в сопровождающей их системе отсчёта они покоятся. Отсюда следует

где dl - пройденный отрезок, или

Соответственно время, измеренное часами, <движущимися по нек-рой траектории АВ, равно след. интегралу по траектории, <по к-рой движутся часы В:

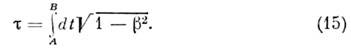
Этот же результат ложно записать в виде

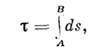
где интеграл берётся по траектории часов. <Из (15) видно, что движущиеся часы всегда отстают от неподвижных. Так жекак и в рассмотренном выше частном случае, справедливость (15) требует, <чтобы ускорения были достаточно малы и не оказывали действия на ход часов. <Из (9) следует закон сложения скоростей. Для частного случая, когда телодвижется в L' параллельно оси х со скоростью V', имеемдля скорости тела в L

где v - скорость L' относительно L. Если рассматривать ф-лу (16) как активное преобразование, тоона описывает буст точки, имевшей первоначально скорость V'. Изэтой ф-лы сразу видна независимость скорости света от движения источника:при V' = с получаем V= с. Из неё также следует ф-лаФренеля частичного увлечения света источником. Если свет распространяетсяв среде с показателем преломления п, движущейся со скоростью v,то V' = с/п и для скорости света в лаб. системе L имеем

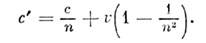
Аберрация света и видимая форма предметовв частной О. т.

Пусть система L' (с осями, параллельнымиосям системы L) движется параллельно оси х системы L соскоростью v и пусть в L' движется импульс света под углом 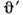к оси х'. Без ограничения общности можно считать, что импульс движетсяв плоскости х'у' и в момент t' =0находится в точке х = у' =0. Из преобразований Лоренца получаем 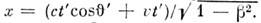Моменту времени t' соответствует в L время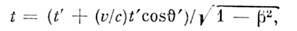

и за это время импульс в L пройдётпуть l = ct. Отсюда для угла луча (соответствующего рассматриваемомуимпульсу света) с осью х и L получаем

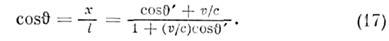
Т. о., движущийся наблюдатель видит объектв др. направлении, чем неподвижный наблюдатель.
Если объект наблюдается под малым телеснымуглом, то изображение предмета, видимое движущимся наблюдателем, сохраняетсвою форму, но оказывается повёрнутым; если наблюдатель в L видитпокоящийся в L' предмет под углом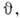 то изображение, к-рое он получит на мгновенной фотографии, будет соответствоватьизображению в L' на снимке под углом 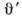(в L' изображение, очевидно, не зависит от момента снимка). Действительно, <пусть импульсы света 1' и 2' в L' дают изображение в L' вмомент t'. Пусть S₁ и S₂- их положения в момент t в L. 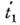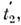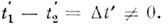В системе L' имсоответствует разное время и Квадрат интервала между S₁ и S₂ равен

где l' - трёхмерное расстояние между S₁ и S₂, равное 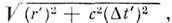r' - расстояние между лучами 1' и 2'. Т. о., s²= -(r'}². В системе L t₁ = t₂,фронт волны перпендикулярен к направлению лучей 1 и 2 и s²= - r², где r - расстояние между лучами в L. Т. к. s - инвариант, то r² = (r')²,что и доказывает сделанное выше утверждение. Более подробно вопрос о видимыхизображениях рассмотрен В. Вайскопфом (V. Weisskopf) и В. Риндлером (W.Rindler) в 1977. Это явление не противоречит, разумеется, сокращению масштабов, <описанному в предыдущем разделе, т. к. там речь шла о мгновенных измерениях, <здесь же решающую роль играет запаздывание импульсов, идущих от разныхточек тела.

Пространство скоростей

Пространством скоростей в частной О. т. <называется пространство, каждой точке к-рого соответствует частица, движущаясяс данной скоростью v, а квадрат расстояния для двух бесконечно близких точек Р, Q равен квадрату ихотносит. скорости, измеренной по часам в Р и Q. Первое утверждениепредполагает введение нек-рой системы отсчёта и в этом смысле координатно-зависимо, <второе имеет абс. смысл. Удобно ввести след. параметризацию. Для коллинеарныхскоростей, как следует из преобразований Лоренца, справедлив закон сложенияскоростей (здесь и ниже будем полагать с= 1, что приводит к существ. <упрощению ф-л):

где v_i - скорость точки1 относительно начала отсчёта 0, v₂ - скорость точки2 относительно точки 1 и r₀₂ - скорость точки 2 относительно0. Эта ф-ла была получена выше для движения частицы по оси х, но, <очевидно, справедлива всегда, если движение происходит по одной прямой. <Введём параметр 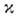такой, что 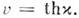Тогда (18) принимает вид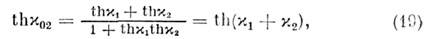

т. е., в отличие от скорости, параметр 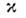аддитивен:

При 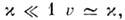откуда следует, что если в пространстве скоростей ввести в качестве радиальнойкоординаты параметр 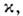то для двух точек, движущихся в одном направлении, квадрат расстояния впространстве скоростей равен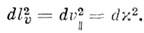

Для точек Р и Q, движущихсяс равными по модулю скоростями, образующими угол 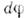,расстояние между ними, если они движутся из одной точки, растёт как 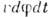во времени покоящейся системы отсчёта. Т. к. dt связано с собств. <временем 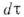для Р, Q соотношением 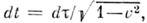то
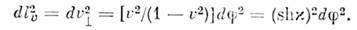
Очевидно, что относит. скорость не зависитот нач. условия (совпадения Р и Q).
В бесконечно малой окрестности точки . пространства скоростей действует закон параллелограмма скоростей Ньютона. <Поэтому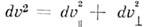 и, следовательно, в случае движения в заданной плоскости

Как известно, такая метрика есть метрикаплоскости Лобачевского. Это - двумерное пространство с постоянной гауссовойкривизной К = -1.
Аналогично, трёхмерному случаю соответствуеттрёхмерное пространство Лобачевского. В пространстве Лобачевского, какво всяком пространстве с заданной метрикой, можно ввести параллельный перенос. Геодезические линии, образуемые параллельным переносом, по определению, <есть прямые в этом пространстве. Т. к. в любой его точке в малой окрестностидействует ньютонов закон сложения скоростей, то в этой окрестности параллельныйперенос означает сохранение направления скорости, а если переносится какой-тодр. вектор, то он должен сохранять угол с направлением скорости. В частности, <параллельному переносу из О в А ( В )координатных осейсоответствует чисто лоренцево преобразование (без вращения) к системе отсчёта, <движущейся со скоростью v₁(v₂) (рис.1). Параллельный перенос вдоль геодезической АВ даёт чисто лоренцевопреобразование от А к В. При этом из-за кривизны пространствасистема, полученная последовательностью переходов ОА, АВ, повёрнута(на угол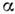 )относительно системы, полученной переходом ОБ. Это отражает тотфакт, что чисто лоренцевы преобразования не образуют группы. Аналогичноможно убедиться, что они не коммутируют между собой.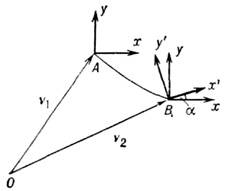

Рис. 1. Система у'х' полученаиз ух параллельным переносом по АВ.

Неевклидовость пространства скоростей непосредственноответственна за явление, наз. томасовской прецессией [Л. Томас (L. Thomas),1926]. Если физически реализованный вектор - ось гироскопа или спин частицы- связан с системой, движущейся ускоренно, а рассматриваемый вектор неиспытывает воздействия к.-л. сил, то он переносится параллельно вдоль годографаскорости, и т. к. пространство имеет кривизну, он прецессирует. Для вычисленияэтой прецессии удобно ввести сопутствующую систему координат, получающуюсяпараллельным переносом из О в Р. При движении из Р в Р' вектор переносится параллельно и по отношению к сопутствующимосям оказывается повёрнутым на угол 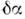= KS_OPP', где К = -1, S_OPP' - площадь ОРР', что даёт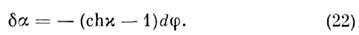

В случае движения по окружности, когда 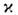=const, для угл. скорости томасовской прецессии имеем

где 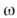- угл. частота. В нерелятивистском пределе Это выражение используется при расчёте тонкой структуры в атомной физике.
С помощью аппарата четырёхмерных векторов, <описанного в след. разделе, легко получить для относит. скорости v₁₂ точек, движущихся со скоростями v₁ и v₂,образующими угол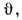 ф-лу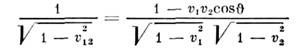

или

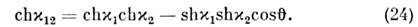
Ф-ла (24) является аналогом ф-лы косинусовсферич. тригонометрии для пространства Лобачевского.

Векторы и тензоры в пространстве Минковского

Для построения инвариантных и ковариантныхвыражений в частной О. т. используется тензорный аппарат в пространствеМинковского. Простейшей величиной, следующей за скаляром, является контравариантныйчетырёхмерный вектор. Таковым является, в частности, 4-вектор 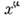с компонентами х⁰ = t, x¹ = x, x²= у, х ³= z. Закон преобразования для него заданф-лами (8). Произвольный 4-вектор 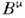,преобразующийся по ф-лам (8), наз. контравариантным. Квадрат его длины 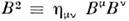является инвариантной величиной.
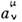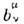Матрицы и связанысоотношением

где

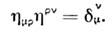
Наряду с контравариантными компонентамивектора 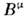можно ввести ковариантные (часто говорят просто о ковариантных векторах)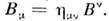Для любых 4-векторов А, В можно определить скалярное произведение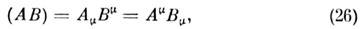

инвариантное относительно преобразованийЛоренца. Произвольный тензор 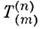ранга п + m с п контравариантными и m ковариантнымииндексами определяется законом преобразования: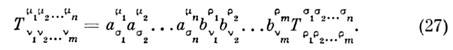

Из определения 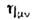следует, что он является инвариантным [переходящим сам в себя при преобразовании(27)] тензором второго ранга (то же относится к ).
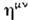Из свойств преобразований Лоренца следует, <что ранг тензора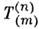 может быть понижен на 2: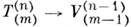свёртыванием (суммированием) по произвольной паре верхних и нижних индексов.
Примерами 4-векторов являются 4-импульссистемы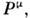 4-потенциал эл.-магн. поля 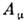и др. Четырёхмерные векторы классифицируются по их поведению относительнонесобств. преобразований Лоренца: полярные векторы меняют знак пространственныхкомпонент, а временная компонента не изменяется; аксиальные векторы ведутсебя противоположным образом. Аналогичная классификация применяется и поотношению к величинам, инвариантным относительно преобразований Лоренца:они делятся на скаляры и псевдоскаляры.
Примером тензоров может служить тензорэнергии-импульса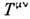 и тензор эл.-магн. поля 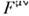.Тензоры второго ранга 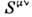могут быть симметричными и антисимметричными, для к-рых соответственно 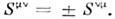Тензор 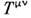является примером тензора первого типа,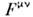- второго.
Рассматривая кинематику точки, движущейсяпо произвольной траектории под действием внеш. сил, удобно ввести в качествепараметра точки Р величину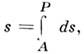 где интеграл берётся по траектории частицы от произвольной точки А,тогда 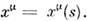В том случае первая производная по s даёт вектор четырёхмерной скорости

Т. к.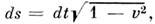то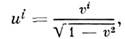

i = 1,2,3,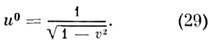

Учитывая, что 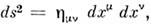и деля это выражение

на ds², получаем

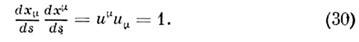
Т. о., квадрат длины 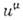равен 1. Инвариантное ускорение определяется как

Из (31) следует, что

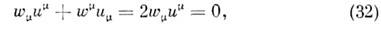
т. е. четырёхмерное ускорение ортогональнок 4-скорости.
Операции дифференцирования и интегрированияв частной О. т. могут быть представлены в ковариантном виде. Взятие частнойпроизводной по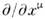 повышает ранг тензора на единицу с появлением ковариантного индекса 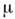(простейший пример - вектор 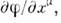где 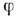- скаляр).
В четырёхмерном мире Минковского возможныодномерные многообразия - линии, двумерные - поверхности, трёхмерные -гиперповерхности и четырёхмерные - объёмы. По всем ним могут производитьсяоперации интегрирования. Инвариантная форма интеграла по линии может иметьвид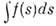 или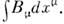
Элементом двумерной поверхности являетсятензор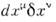 - 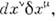соответственноинвариантный интеграл возникает при интегрировании с антисимметричным тензором. <Элемент гиперповерхности, построенный на 4-векторах dx(1), dx(2), dx(3 )(где числа в скобках нумеруют 4-векторы), имеет вид детерминанта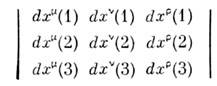

и является тензором третьего ранга. В этомслучае удобно ввести полностью антисимметричный тензор 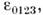такой, что 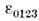= 1, а при каждой перестановке индексов знак меняется. Этот тензор инвариантенпри собственных преобразованиях Лоренца (но меняет знак при замене t- t или r- r). С его помощью объёму гиперповерхности можно поставить в соответствиевектор 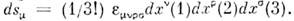Для случая, когда гиперповерхность - пространственная область с t =0, у 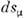отлична от нуля только компонента ds₀, а если dx(1),dx(2), dx(3 )направлены по осям х, у,z, то

ds₀ =dxdydz = dx^ldx²dx³,

т. е. ds₀ равна элементутрёхмерного объёма. Элемент четырёхмерного объёма может быть представленв виде 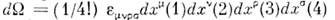либо 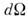= dx⁰ dx¹ dx² dx³, т. <е. он является четырёхмерным скаляром. Так же как в трёхмерном пространстве, <в четырёхмерном пространстве существуют теоремы Гаусса и Стокса, напр.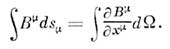

Спинорные представления группы Лоренца

Из 4-вектора х ⁰, х¹, х ², х ³ можно составить эрмитову матрицу

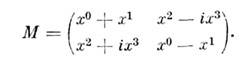
Детерминант этой матрицы представляет собойинтервал (x⁰)² - (х ¹)²-( х ²)²- ( х ³)². Еслиумножить М справа на произвольную унимодуляриую матрицу (матрицус детерминантом единица) К, а слева на эрмитово сопряжённую . матрицу К ⁺ ( М' = K+ МК), то очевидно, что этопреобразование сохраняет как эрмитовость, так и детерминант матрицы М. Действительно, ( М')⁺ = (К ⁺ МК)⁺= К ⁺ МК = М',det М' = det К⁺det Мdet К = detМ.
Т. о., если записать матрицу М' ввиде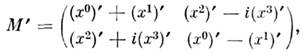

то получим s² = (s')²,т. е. преобразование, принадлежащее группе Лоренца. Очевидно, что так построенныепреобразования образуют группу. Можно показать, что каждому собств. преобразованиюЛоренца соответствуют две и только две матрицы К, отличающиеся лишьзнаком. Возможность найти для каждого преобразования Лоренца подходящуюматрицу К следует, по существу, из того, что унимодулярная матрицазависит от стольких же параметров, что и группа Лоренца, а неоднозначностьв знаке матрицы К очевидна. Если ввести двух-компонентную величину 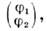преобразующуюсяпри преобразованиях Лоренца с помощью матрицы К, то получится новыйвид представления группы Лоренца - спинорный. Он возникает естественнопри построении Дирака уравнения, описывающего частицы со спином ¹/₂ в квантовой теории поля.

Структура пространства Минковского

Из ф-л (9) и (10) следует, что в частнойО. т. время события не является абс. величиной: события, происходящие вразных точках, будут иметь разные времена в различных и. с. о., даже еслиони были одновременны в исходной системе отсчёта. Если |x _А- x _В|>|t _А - t _В|,(33) то временной порядок событий А, В может меняться припереходе от системы L к системе L'. В этом нет логич. противоречия, <если скорость света является предельной для распространения сигналов ивзаимодействии, т. к. тогда при выполнении условия (33) события А и В не могут быть причинно связаны. Напротив, если | х _А- х _В|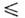|t_A- t_B|, возможна причинная связь между А и В, нов этом случае порядок событий не меняется. (Однако если бы существоваличастицы, движущиеся со скоростью, большей скорости света, - т. н. тахионы, то порядок причинно связанных событий мог бы быть разным в разных системахотсчёта. Это приводило бы к серьёзным затруднениям с причинностью, т. к. <наблюдатель в L' мог бы "уничтожить" событие А, к-рое в . порождает событие В, и причинная связь нарушилась бы. Попыткипереинтерпретпровать теорию тахионов так, чтобы она стала непротиворечивой, <не привели к успеху.)
Невозможность движения сигналов со скоростью, <большей скорости света, не означает, что в частной О. т. вообще невозможныдвижения со сверхсветовой скоростью. Такие движения могут быть реализованы, <напр., как движение "зайчика" от прожектора, но в этом случае взаимодействиеи причинная связь между разными точками траектории "зайчика" отсутствуют.
Инвариантная запись (33), справедливаяв любой системе отсчёта, имеет вид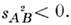 Такие интервалы наз. пространственноподобными. В подходящей системе отсчётасоответствующий им 4-вектор АВ может быть представлен в виде (0,r). Условие 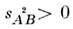определяет времениподобные интервалы; соответствующий вектор может бытьпредставлен в виде (t,0), и время t - это время, отсчитанноечасами, движущимися по прямой АВ. Ур-ние s² = 0 соответствуетпрямой, являющейся траекторией светового луча или любой безмассовой частицы. <Относительно любой точки О трёхмерное многообразие, наз. световымконусом или световой гиперповерхностью, на к-рой лежат все световыелучи, проходящие через О, разбивает пространство на две области:

Если принять О за начало отсчёта, <то в силу того, что собств. преобразования Лоренца не меняют направлениявремени внутри светового конуса и на нём самом (34а), световой конус изаключённый внутри него объём можно разбить на части, соответствующие .t <0, наз. верхней и нижней полами. Часть <0,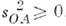, соответствует событиям, на к-рые О может оказать причинное воздействие, <или точкам, в к-рые может прийти сигнал из О; это абс. будущее для О. Соответственно, события, относящиеся к нижней поле, - совокупностьвсех событий, к-рые О может увидеть, или тех, к-рые могут оказатьна неё причинное действие. Т. о., эта пола - абс. прошлое для О. Всетраектории тел и лучей, приходящих в О, должны принадлежать нижнейполе t< 0,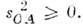Соответственно, все лучи света и траектории тел, выходящих из О,принадлежат верхней поле и образуют абс. будущее для О.
Совокупность точек, связанных с О векторами(0, х, у, z) в системе отсчёта L, где точкипо оси времени имеют вид (t,0), т. е. в системе, где ось временипроходит через О, очевидно, соответствует гиперповерхности, ортогональнойк оси времени в метрике Минковского. Она состоит из событий, одновременныхс О и образующих трёхмерное евклидово пространство. Такое пространствоможно построить для любой точки на осп времени. Телам, покоящимся в этомпространстве, отвечают прямые мировые линии, параллельные оси времени.
Траектории любого тела, движущегося прямолинейнои равномерно в системе L и проходящего через О при t=0, можио принять за временную ось системы отсчёта L', связаннойс L преобразованием Лоренца. Единичный вектор e_t, направленный по оси времени, всегда удовлетворяет инвариантному условию

Для оси t он имеет вид (1, 0, 0,0), а произвольный вектор, направленный по этой оси, есть te_t= (t,0, 0, 0). Для оси t' единичный вектор е'_t равен 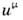скомпонентами 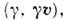соответственно, произвольный вектор, направленный по t', имеет вид t'u 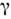= (t',t'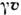). Совокупность всех векторов, ортогональных оси t' в заданнойточке, образует пространство системы L', и события, лежащие в нём. <одновременны в L'. Если в данной точке t' в этом пространствепостроить оси х', y', z', то они образуют полный набор координатв L'. Ось х' можно поместить в плоскость tt' (рис.2), тогда единичный вектор, направленный по x', будет иметь вид е' _х (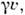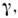0,0); в метрике Минковского он ортогонален е' _х.
Отсюда сразу вытекают эффекты измененияинтервалов времени и пространства при переходе от L к L'. Промежутоквремени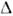 t' в L' имеет временную компоненту в L, равную временнойкомпоненте вектора 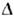t'е'_t,что даёт 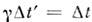или

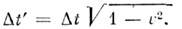
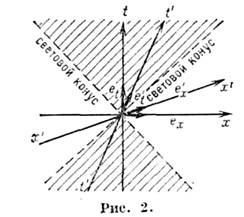
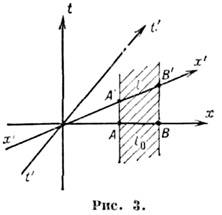
Соответственно, чисто пространственныйотрезок АВ длины l₀ в L описывает в миреМинковского полосу, показанную на рис. 3; точки пересечения её границ сосью х' одновременны с точки зрения L' и, следовательно, <определяют длину l отрезка АВ вдвижущейся сиcтеме. <Но l₀ - это компонента вектора 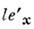пооси x, т. е.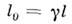или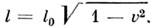

Релятивистская механика

Для всех известных в частной О. т. классич. <полей и частиц ур-ния движения могут быть получены из условия равенстванулю вариации действия:

Величина S являетсячетырёхмернымскаляром и может быть представлена в виде

где L - плотность ф-ции Лагранжа(лагранжиан). Для свободной материальной точки массы m

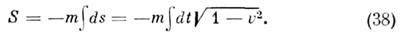
Условие экстремума даёт

Величина 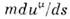наз. 4-импульсом частицы.
Релятивистская инвариантность требуетинвариантности действия для замкнутой системы относительно группы Пуанкаре. <Инвариантность относительно подгруппы сдвигов приводит, в силу теоремыНётер, к четырём законам сохранения:

конкретный вид тензора 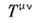определяется видом L. Легко показать, что 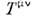всегдаможет быть приведён к симметричному виду. Из (40) следует существованиечетырёх сохраняющихся величин:

где интеграл берётся по трёхмерной гиперповерхности. <Величины 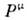образуют 4-импульс; компонента Р° - энергия системы, Р ⁱ(i=1, 2, 3) - компоненты её импульса. При интегрировании в (41) можновзять любую гиперплоскость или даже искривлённую пространственноподобнуюгиперповерхность, делящую мир Минковского на две части. Выбирая в качествегиперповерхности гиперплоскость х⁰= const, получаем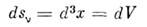

и

Вектор 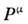времениподобен, поэтому всегда можно систему отсчёта, в к-рой определеноинтегрирование в (42), выбрать так, что Р ⁱ =0. Эту системуназывают системой покоя для рассматриваемого тела. В ней, по определению,4-скорость тела равна (1,0). Введём массу тела, определив её в системепокоя как

Отсюда следует, что в системе покоя

В силу релятивистской инвариантности этосправедливо в любой системе отсчёта, если массу считать скаляром. Переходяв систему отсчёта, движущуюся со скоростью v, получаем

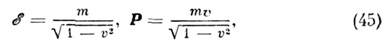
т. е.

Это соотношение справедливо и для безмассовыхчастиц, для к-рых v - единичный вектор. Случай m =0получаютпредельным переходом. В системе единиц с с 1 ф-лы (45), (46) принимают вид: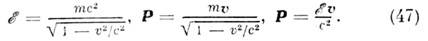

Многие авторы, пытаясь сохранить ньютоновосоотношение между импульсом и энергией ( Р = mv), наз. величину 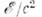полной массой, релятивистской массой или просто массой и обозначают её т(v), т _r или m, а обычную массу, к-раяв этой статье обозначается т, наз. массой покоя (обозначают m₀).Т. о. в их обозначениях т = т _r = m (v) =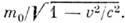Введение m(v), однако, излишне, т. к. приводит к необходимости говоритьо двух законах сохранения: энергии и полной массы, тогда как второй изних есть просто закон сохранения энергии, поделённой на с ². Кроме того, ф-лы (47) неприменимы к безмассовым частицам.
Для материальной точки состояние движенияоднозначно определяется вектором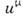 ,и 4-импульс (введённый описанным выше способом) равен 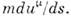Если п первоначально изолированных друг от друга тел (систем) вступаютв нек-рой области пространства-времени во взаимодействие, после чего возникают п' новых тел, то, поскольку до взаимодействия полный 4-импульс 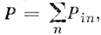а после взаимодействия 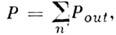где P_in и P_out обозначают начальные(входящие) и конечные (выходящие) частицы, и поскольку полный импульс сохраняетсявсегда,

В частности, для энергии имеем

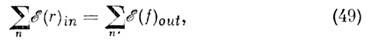
где r и f нумеруют входящиеи выходящие частицы.
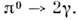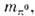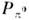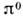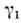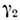В отличие от энергии сумма масс не сохраняется, <но полная масса замкнутой системы, разумеется, сохраняется в любом процессе. <Напр., в физике элементарных частиц хорошо известен процесс распада Нач. сумма масс есть просто а конечная равна нулю. Если обозначить 4-пмпульс ,a k₁, k₂ -4-импульсы и ,то 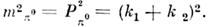В системе центра инерции двух 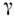: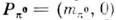, k₁ = (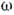,k),k₂ = (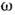,- k), |k|=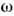,окончательно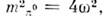 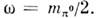Из (48) следует, что если покоящемуся телу сообщают энергию 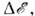то его масса возрастает на ту же величину, 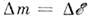(предполагается, <что сообщаемый телу импульс равен нулю), н, наоборот, если тело теряетэнергию 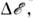оставаясь в покое, то его масса уменьшается на
В нсрелятивистском пределе энергия в (49) может быть записана в виде m + mv²/2 изакон сохранения энергии принимает вид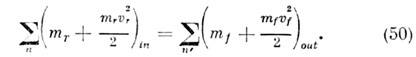

Напр., в распаде урана его масса покоябольше сумм масс покоя осколков; разность масс выделяется в виде их кинетич. <энергий.
Из (39) следует, что для любого тела

Использование 4-импульса существенно упрощаетрешение задач с релятивистской кинематикой. Так, при распаде частицы смассой т₀ на частицы с массами т₁, т₂ получаем Р ₀ = Р₁ + Р ₂ или Р₀ - Р₁ = Р₂(52) Возводя в квадрат (52), получаем
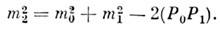
В системе покоя частицы с массой т ₀ имеем (P₀P₁) =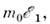откуда 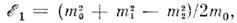и аналогично для
Для системы, находящейся во внеш. поле,4-импульс не сохраняется. Для точечной частицы массы т закон егоизменения можно представить в виде

где 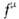- четырёхмерная внеш. сила. В электродинамике 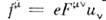(сила Лоренца) и ур-ние движения для частицы в поле имеет вид

( е - электрич. заряд частицы).

Экспериментальные основания частнойО. т.

Первоначальной эксперим. основой частнойО. т. был ряд оптич. экспериментов, установивших отсутствие эффектов, связанныхс движением Земли относительно гипотетич. эфира в порядках v/c и(v/с)² (последнее - в опыте Майкельсона - Морли в 1887;см. Майкельсона опыт). Именно основываясь на этих опытах, А. Пуанкарев 1895 высказал гипотезу, что постулат относительности точен во всех порядкахпо v/c. К 1905, когда Лоренц, Пуанкаре и Эйнштейн дали свои формулировкичастной О. т., отсутствие эффектов в порядке v/c нашло дополнит. <подтверждение в ряде опытов, но отсутствие эффектов в порядке (v/c)² подтверждалось только опытом Майкельсона - Морли.
Постулат независимости скорости светаот движения источника подтверждения на опыте не имел; он был выдвинут Эйнштейномкак следствие справедливости электродинамики Лоренца в системе эфира ипринципа относительности, исходя из к-рого этот постулат переносится налюбые и. с. о.
Опыты Майкельсона - Морли неоднократноповторялись в 20-е гг. и неизменно давали отрицат. результат. С появлениеммазеров возникла возможность проверки отсутствия эффектов в порядке v/c в распространении света [Седерхольм (Y. P. Cederholm) и др., 1964].Достигнутая точность порядка 10^-3.
Независимость скорости света от движенияисточника неоднократно проверялась, наиб. точно - в работе Т. Альвегера(Т. Alvager) с сотрудниками (1964). В этом опыте измерялась скорость фотоновот распада p⁰ -мезоновс энергией ок. 1 ГэВ, т. е. движущихся со скоростью, практически равной с. При этом скорость движущихся вперёд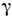 -квантовсовпадала со скоростью света с точностью порядка 10^-4.
В 1986 проверялась ф-ла релятивистскогоэффекта Доплера: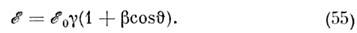

Достигнутая точность для совпадения отношения с теоретически предсказанной величиной [ф-ла (55)] составляет 1,00004(27),т. е. ~ 3 х 10^-4. В принципе точность опыта может быть доведенадо 10^-7.
Ставились опыты по проверке отд. следствийчастной О. т. Так, эффект замедления времени был проверен С. Росси (S.Rossi) с сотрудниками (1942) [III, 3] вплоть до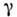 ~10.Полученный результат, включая зависимость времени жизни от ,согласуется с предсказаниями О. т.
В ядерной физике проверялось соотношениемежду дефектом массы и выделяющейся в реакции энергией. В особо прецизионныхопытах Н. Смит (N. Smith, 1939) [III, 1] показал, что выделяющаяся энергиясоответствует дефекту массы с точностью ~0,01.
В совр. технике широко применяются такиеустройства, как электронно-лучевые трубки, электронные микроскопы и др.,в к-рых достигаются 1. Для расчёта таких устройств применяются ф-лы релятивистской механики, <и в этом смысле частная О. т. является такой же основой инженерных расчётов, <как механика Ньютона - основой для расчётов кораблей, самолётов, мо-

стов и др. "нерелятивистских" сооружений. <Наибольшие достигаютсяв совр. ускорителях заряж. частиц: для протонов 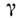~ 10³, для электронов 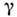~ 10⁵. При этом наглядно демонстрируется тот факт, что скоростьсвета является предельной для всех частиц: после того как 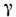становится больше 10, энергия частиц растёт, а скорость не изменяется, <становясь практически равной скорости света.
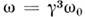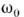Одним из наиб. ярких релятивистских эффектов, <наблюдаемых на электронных циклич. ускорителях больших энергий (синхротронах),является релятивистский рост частоты синхротронного излучения; релятивистскиеэффекты приводят к тому, что частота синхротронного излучения имеет резкиймаксимум при , где - угл. частота движения электронов. Этот эффект хорошо наблюдается. Релятивистскоезамедление времени лежит в основе технологии получения вторичных пучковнестабильных частиц: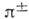,,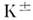,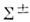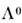и др. Напр., в состоянии покоя 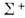-и 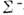-гипероны живут соответственно 0,8 х 10^-10 с и 1,5 х 10^-10 с, но уже при 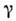~10 они, двигаясь со скоростью v= с, имеют длины распада 24 сми 45 см, что делает возможным формирование 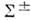-пучков. <Ещё сильнее проявляется замедление времени в пучках 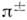-мезонов, <где достигается 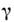~10³ и выше.
Точность релятивистской кинематики можнооценить по точности в определении масс нестабильных частиц (~ 10^-4- 10^-5.) Здесь производится проверка кинематики на самосогласованность, <поэтому приведённая ошибка в определении масс может рассматриваться какоценка точности релятивистской кинематики.
Геометрия Минковского лежит в основе совр. <теорий взаимодействия элементарных частиц - квантовой электродинамики (КЭД), квантовой хромодинамики и теории электрослабого взаимодействия, объединяющей КЭД и теорию слабого взаимодействия. Из перечисленныхтеорий лучше всего на опыте проверена КЭД, относительно к-рой из прямыхопытов известно, что она справедлива вплоть до расстоянии 10^-16 см и соответственно времён ~10^-26 с. Вплоть до таких расстоянийи времён действует, т. о., геометрия Минковского.

Лит.:1.Труды классиков:1) Принцип относительности, Г. Лоренц, А. Пуанкаре, А. Эйнштейн, Г. <Минковский. Сб. работ, М. - Л., 1935; 2) Лоренц Г. А., Старые и новые проблемыфизики. [Сб. пер.], М., 1970; 3) Пуанкаре А., Избр. труды, т. 3, М., 1974;4) Эйнштейн А., Собр. научных трудов, т. 1 - 2, М., 1965 - 66. II. Монографии:1) Борн М., Эйнштейновская теория относительности, пер. с англ., 2 изд.,М., 1972; 2) Вавилов С. И., Экспериментальные основания теории относительности, <М. - Л., 1928; 3) Вайскопф В., Физика в двадцатом столетии, пер. с англ.,М., 1977; 4) Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988;5) Логунов А. А., Основы теории относительности, М., 1982;
6) Rindler W., Essential relativity, 2ed., N. Y., 1977; 7) Паули В., Теория относительности, пер. с нем., 2 изд.,М., 1983; III. Периодические издания: 1) Srаith N. М., The energiesreleased in the reactions Li (p,a)He⁴ and Li^u(d,a) He⁴ and masses of the light atoms, "Phys. Rev.",1939, v. 56, p. 548; 2) Rоssi В. и др., Farther measurements of the mesotronlifetime, "Phys. Rev.", 1942, v. 61, p. 675; 3) Review of particle properties.Particle data group, "Rev. Mod. Phys.", 1984, v. 56, N° 2, pt 2; 4) A1vagеrТ. и др., Test of a second postulate of special relativity in the GeV region,"Phys. Lett.", 1964, v. 12, p. 260; 5) Сedаrhо1m ,J. P. и др., New experimentaltest of special relativity, "Phys. Rev. Lett.", 1958, v. 1, p. 342; 6)Мас Arthur D. W. и др., Test of a special-relativistic Doppler formulaat p = 0,84, "Phys. Rev. Lett.", 1986, v. 56, p. 282.

И. Ю. Кобзарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.