ЛАПЛАСА МЕТОД

ЛАПЛАСА МЕТОД

асимптотических оценок - метод вычисления асимптотики при l>0, интегралов Лапласа

где W=[a, b] - конечный отрезок, S - действительная, f - комплексная функции, достаточно гладкие при Асимптотика F(l) равна сумме вкладов от точек, в к-рых достигается если число их конечно.

1) Если максимум достигается при х=а и то вклад от точки ав асимптотику интеграла (1) равен

2) Если максимум достигается во внутренней точке х 0 отрезка 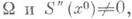то вклад от нее равен

Эта формула получена П. Лапласом [1]. Полностью исследован случай, когда функции f(x), S' (х).имеют нули конечной кратности в точках максимума функции S, и получены асимптотич. разложения (см. [2] - [8]). Л. м. распространяется и на случай контура W, расположенного на комплексной плоскости (см. Перевала метод).

Пусть W - ограниченная область в наибольшее значение функции S(x).в замыкании W достигается только во внутренней точке х 0, и х 0 - невырожденная стационарная точка функции S. Тогда

В этом случае также получены асимптотич. разложения для F(l). Все приведенные выше формулы справедливы при комплексных Имеются также модификации Л. м. на случай более сложной зависимости от параметра (см. [4], [8]):

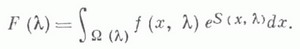
Лит.:[1] Laplace P. S., Essai philosophique sur les probabilites, CEuvres completes, t. 7, P., 1886 (в рус. пер.- Опыт философии теории вероятностей, М., 1908); [2] Эрдейи А., Асимптотические разложения, пер. с англ., М., 1962; [3] Б р ё й н Н. Г., Асимптотические методы в анализе, пер. с англ., М., 1961; [4] Евграфов М. А., Асимптотические оценки и целые функции, 2 изд., М., 1962; [5] Копсон Э.-Т., Асимптотические разложения, пер. с англ., М., 1966; [6] О 1 v е r P. W. J., Asymptotics and special functions, N. Y.- [а. о.], 1974; [7] Риекстыньш Э. Я., Асимптотические разложения интегралов, т. 1, Рига, 1974; [8] Федорюк М. В., Метод перевала, М., 1977. М. В. Федорюк.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "ЛАПЛАСА МЕТОД" в других словарях:

  • Метод перевала — метод, использующийся для аппроксимации интегралов вида где это некоторые мероморфные функции, это некоторое большое число, а контур может быть бесконечным. Этот метод часто называется обобщением метода Лапласа. Содержание …   Википедия

  • Метод Лапласа — метод, использующийся для аппроксимации интегралов вида где это некоторая дважды дифференцируемая функция, это некоторое большое число. Идея метода Лапласа Предполагается, что функция имеет единственный глобальный ма …   Википедия

  • Метод граничных элементов — Метод конечных элементов: триангуляция Метод конечных элементов (МКЭ) численный метод решения задач прикладной механики. Широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электромагнитных… …   Википедия

  • Метод наименьших модулей — (МНМ) один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки. МНМ применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто… …   Википедия

  • Метод стационарной фазы — Метод стационарной фазы  метод, использующийся для аппроксимации интегралов вида: Содержание 1 Основы 2 Пример 3 Книги …   Википедия

  • ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — интегральное преобразование где интегрирование ведётся по контуру L в комплексной плоскости переменной z=x+iy, ставящее в соответствие ф ции f(z), определённой и интегрируемой на L, аналитич. ф цию F(k )комплексной переменной . Л. п. в более… …   Физическая энциклопедия

  • Метод конечных элементов — Решение методом конечных элементов двухмерной магнитостатической задачи (линии и цвет означают направление и величину магнитной индукции) …   Википедия

  • ЛАПЛАСА УРАВНЕНИЕ — численные методы решения методы, заменяющие исходную краевую задачу дискретной задачей, содержащей конечное число N неизвестных, нахождение к рых с соответствующей точностью позволяет определить решение исходной задачи с заданной точностью… …   Математическая энциклопедия

  • МЕТОД ГЕНЕТИЧЕСКИЙ — (от греч. genesis происхождение) способ исследования соц. явлений и процессов, основанный на анализе их происхождения и развития. Г.м. предполагает сведение многообразия явлений к фундаментальным, исходным элементам (или состояниям) и выведение… …   Российская социологическая энциклопедия

  • ПЕРЕВАЛА МЕТОД — метод вычисления асимптотики интегралов вида (*) где большой параметр, у контур в комплексной плоскости z, функции f(z).и S(z) голоморфны в области D, содержащей у. Нули функции S (z) наз. точками перевала функции S(z); точка перевала седловая… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»