ОРЛИЧА ПРОСТРАНСТВО

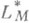- банахово пространство измеримых функций; введено В. Орличем [1]. Пусть М(и).и N(и) - пара дополнительных N-функций (см. Орлича класс).и G - ограниченное замкнутое множество в . Пространством Орлича наз. множество измеримых относительно меры Лебега фуниций на G, на к-рых

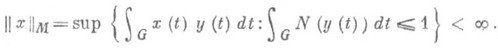
О. п.- полнее нормированное пространство относительно нормы || х||_M, к-рая наз. нормой Орлича. Когда М(и)=иР,, то совпадает с Рисса пространством L_p и с точностью до скалярного множителя || х||_M совпадает с ||x||L_p.

Если M₁(u).и M₂(u).суть N-функции, то вложение имеет место тогда и только тогда, когда для нек-рого Си всех достаточно больших ивыполнено неравенство . Для любого О. и. справедливы вложения . Всякая суммируемая функция принадлежит нек-рому О. п.

Пространство 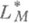сепарабельно тогда и только тогда, когда М(и).удовлетворяет D₂ -условию. В общем случае 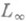не плотно в и замыкание 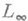в 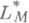обозначается через Е _M, оно всегда сепарабельно. Если , то

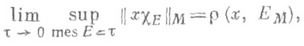
где

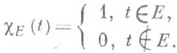
Если М(и).и N(и) - дополнительные N-функции и , , то справедлив аналог Гёлъдера неравенства

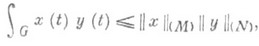
где ||x||(M) - Люксембурга норма. Всякий непрерывный линейный функционал f на Е _M представим в виде

где и ||f||= ||у||_(N)

Критерии компактности М. Рисса (М. Riesz) и А. Н. Колмогорова для пространств L_p переносятся на Е _М. Следующие условия эквивалентны: 1) пространство рефлексивно; 2) М(и).и N(и).удовлетворяют D₂ -условию; 3) в 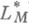существует безусловный базис;

4) Хаара система образует безусловный базис в ;

5) тригонометрич. система - базис в . Система Хаара - базис в ЕМ.

Аналогичным образом определяется пространство последовательностей , однако свойства пространства зависят от асимптотики функции М(и).в 0. Изучены [5] многие геометрич. свойства пространств 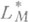и 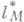;напр., для любой функции М(и).находится множество всех таких р, что l _р изоморфно вкладывается в .

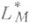О. п. применяются при изучении свойств интегральных операторов, в теории дифференцируемых функций многих переменных и в других разделах анализа.

Лит.:[1] Orlicz W. , "Bull, intern. Acad. Pol. Ser. A", 1933 (annee 1932), p. 207-20; [2] Красносельский М. А., Рутицкий Я. Б., Выпуклые функции и пространства Орлича, М., 1958; [3] Гапошкин В. Ф., "Функц. анализ и его прилож.", 1967, т. 1, № 4, с. 26-32; [4] Крейн С. Г., Петунин Ю. И., Семенов Е. М., Интерполяция линейных операторов, М., 1978; [5] Lindenstrauss J.,Tzafriri L., Classical Banach Spaces, v. 1 - 2, В.- Hdlb.- N. Y., 1977-79.

Е. М. Семенов.