- ОРНСТЕЙНА - ЧЕКОНА ЭРГОДИЧЕСКАЯ ТЕОРЕМА
пусть (W,m) - пространство с s-конечной мерой и T - линейный положительный оператор в L1(W,m), причем L1 -норма ||T||
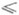 1; если f,
1; если f,  и
и  почти всюду, то предел
почти всюду, то предел
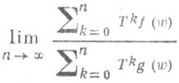
существует почти всюду на том множестве, где знаменатель при достаточно больших n отличен от нуля, т. е. где хоть одно из чисел
 .
.
Эта теорема сформулирована и доказана Д. Орнстейном и Р. Чековом [1] (см. также [2], [3]); позднее был получен ее аналог для непрерывного времени (см. [4]).
Непосредственными следствиями О.-Ч. э. т. являются Биркгофа эргодическая теорема и нек-рые из ранее предложенных обобщений последней, но имеется также ряд эргодич. теорем, независимых от О.-Ч. э. т., а сама она подвергалась различным обобщениям (см. [5], [6], а также лит. при ст. Операторная эргодическая теорема). Вместе с тем из всех обобщений теоремы Биркгофа, по-видимому, чаще всего используется О.-Ч. э. т.
В иностранной литературе О.-Ч. э. т., как и вообще теоремы, в к-рых речь идет о пределе отношения двух временных средних, наз. ratio ergodic theorem.
Лит.:[1] Сhасоn R. V., Ornstein D. S., "III. J. Math.", 1960, v. 4, № 2, p. 153-60; [2] Xопф Э., "Математика", 1962, т. 6, № 3, с. 29-36; [З] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969; [4] Akсоglu М. А., Сunsоlо J.., "Proc. Amer. Math. Soc.", 1970 v. 24, № 1, p. 161-70; [5] Сhасоn R. V., в кн.: Ergodic theory. Proceedings of an International Symposium. New Orleans, 1961, N. Y.- L., 1963, p. 89-120; [6] Теrrе11 T. R., "Boll. Unionemat. ital.", 1972, v. 6, №2, p. 175-80. Д. <В. <Аносов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
