ОПТИМАЛЬНОГО БЫСТРОДЕЙСТВИЯ ЗАДАЧА

одна из задач оптимального управления математической теории, состоящая в определении минимального времени

(1)
за к-рое управляемый объект, движение к-рого описывается системой обыкновенных дифференциальных уравнений

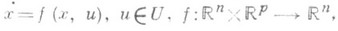
можно перевести из заданного начального состояния x(0)=x₀ в заданное конечное состояние х(t₁)=x₁ Здесь x=x(t).есть n-мерный вектор фазовых координат, а u=u(t).есть р-мерный вектор управляющих параметров (управлений), принадлежащий при любом ( заданной замкнутой допустимой области управлений U.

Искомое минимальное время t₁ является функционалом (1), зависящим от выбираемого управления u(t). В качестве класса допустимых управлений, среди к-рых разыскивается управление, оптимальное по быстродействию, для большинства приложений достаточно рассматривать кусочно непрерывные управления u(t), т. е. функции, непрерывные для всех рассматриваемых t, за исключением конечного числа моментов времени, в к-рых они могут терпеть разрывы 1-го рода. Теоретически, строго говоря, следует рассматривать более общий класс функций u(t). , измеримых по Лебегу.

О. б. з. можно рассматривать как частный случай Вольца задачи и Майера задачи, рассматриваемых в вариационном исчислении, получающийся из этих задач при специальном задании оптимизируемого функционала. Оптимальное по быстродействию управление и(t).должно удовлетворять принципу максимума Понтрягина, являющемуся необходимым условием, обобщающим необходимые условия Эйлера, Клебша и Вейерштрасса, используемые в классическом вариационном исчислении.

Для линейных О. б. з. из необходимых условий можно получить нек-рые выводы о качественной структуре оптимального управления. Линейным и О. б. з. (см. [1], [2]) наз. такие задачи, в к-рых выполнены следующие три условия:

1) уравнения движения объекта линейны по хи и:

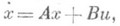
где Аи В- постоянные матрицы размерности пХпи nХр соответственно;

2) конечное состояние x₁ совпадает с началом координат, являющимся состоянием равновесия объекта при u=0;

3) область управления Uявляется р-мерным выпуклым многогранником таким, что начало координат пространства ипринадлежит U, но не является его вершиной.

Пусть выполнено условие общности положения, состоящее в линейной независимости векторов

где w - произвольный р-мерный вектор, параллельный ребру многогранника U. Тогда для оптимальности по быстродействию управления u(t)., переводящего объект из заданного начального состояния х ₀ в положение равновесия (начало координат в пространстве х), необходимо и достаточно, чтобы оно удовлетворяло принципу максимума Понтрягина. Далее, оптимальное управление и(t).в линейной задаче оптимального быстродействия кусочно постоянно, и его значениями являются лишь вершины многогранника U.

В общем случае число переключений u(t).хотя и конечно, но может быть произвольным. В следующем важном случае число переключений допускает точную оценку сверху.

Если многогранник Uявляется р-мерным параллелепипедом

и все собственные значения матрицы Адействительны, то каждая на компонент u^s(t),s=1,..., р, оптимального управления и(t).является кусочно постоянной функцией, принимающей только значения а ^s и b^s и имеющей не более п-1 переключений, т. е. не более пинтервалов постоянства.

О. б. з. может рассматриваться и для неавтономных систем, т. е. для систем, у к-рых правая часть f зависит еще и от времени t.

В тех случаях, когда это удается, полезно рассматривать О. б. з. не только в программной постановке, как это описано выше, но и в позиционной постановке в форме задачи синтеза (см. Оптимальное управление позиционное). Решение задачи синтеза позволяет получить качественное представление о структуре оптимального по быстродействию управления, переводящего систему из любой точки, находящейся в нек-рой окрестности исходной начальной точки х ₀, в заданное конечное состояние х ₁.

Лит.:[1] Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф., Математическая теория оптимальных процессов, 3 изд., М., 197В; [2] Болтянский В. Г., Математические методы оптимального управления, М., 1966. И. Б. Вапнярский.