ОБРАЩЕНИЕ МАТРИЦЫ

- алгоритм, применяемый при численном нахождении обратной матрицы. Как и в задаче решения линейных систем, методы численного обращения подразделяются на прямые и итерационные; однако итерационные методы вследствие их трудоемкости играют здесь существенно меньшую роль.

Большинство прямых методов О. м. основано на идее разложения заданной матрицы в произведение легко обращаемых сомножителей. Если

- такое разложение, то

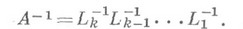
Типичным (и одним из наиболее употребительных) прямых методов О. м. является метод Жордана (см. [1]).

Пусть А- невырожденная матрица порядка п. Построение обратной матрицы А ^-1 происходит в пшагов; результатом k-го шага будет матрица , первые кстолбцов к-рой совпадают с одноименными столбцами единичной матрицы. Переход от (пусть А=А ₀ )к 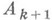с матричной точки зрения эквивалентен умножению .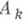слева на матрицу , к-рая отличается от единичной лишь (k+1)-м столбцом. Элементы этого столбца выбираются так, чтобы привести (k+1)-й столбец к единичному, и имеют вид

Из соотношений

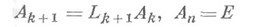
вытекает

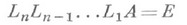
и

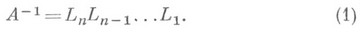
Получение факторизованного представления (1) для обратной матрицы требует примерно операций умножения и примерно операций сложения. Приблизительно такое же число дополнительных операций необходимо для того, чтобы перемножить матрицы в (1) и получить явный вид . Во многих приложениях операции О. м. использование факторизованной формы (1) столь же удовлетворительно, что и явного вида. Напр., вычисление произведения , где b- вектор-столбец, требует одинаковой арифметич. работы в обоих случаях. Одинаковы и требования к памяти при реализации на ЭВМ.

В приведенном описании метода Жордана предполагалось для простоты, что все элементы (называемые ведущими элементами) отличны от нуля. В действительности метод Жордана, как и методы типа Гаусса для решения линейных систем, как правило, применяется с той или иной схемой выбора ведущих элементов. Использование такой схемы равносильно введению в (1) дополнительных множителей, учитывающих перестановки строк и столбцов обратной матрицы. Точность вычисленного решения, как и в случае линейных систем, зависит от степени роста матричных элементов на промежуточных шагах метода. Такой рост и, следовательно, ухудшение точности вычисляемого решения в методе Жордана, даже при выборе ведущего элемента, более вероятны, чем в методах типа Гаусса.

Невязкой, соответствующей приближенной обратной матрице Xдля А, наз. матрица . Имеет место оценка

Таким образом, норма невязки является оценкой относительной точности приближенной обратной матрицы X. В этом состоит важное отличие задачи численного О. м. от задачи решения линейных систем, где (напр., в ортогональных методах или методах типа Гаусса) невязка обычно мала, а качество полученного решения зависит от обусловленности системы.

Обращение ряда важных классов матриц может быть достигнуто значительно более экономичными, чем в общем случае, методами. Таковы теплицевы, ганкелевы, ленточные (и, в частности, трехдиагональные) матрицы, блочные матрицы, имеющие теплицеву структуру или структуру кронекерова произведения, и т. д. Напр., пусть Т- теплицева матрица порядка n+1 с элементами из Rили С:

Предполагается, что не только Т, но и ее главная подматрица порядка пневырождены. Тогда для матрицы уже, вообще говоря, не являющейся теплицевой, справедливо представление (см. [2]):

При этом векторы

суть соответственно первый и последний столбцы Таким образом, Тполностью определяется заданием первого и последнего столбцов. При необходимости из (2)могут быть последовательно вычислены все элементы

Это вычисление требует арифметич. операций.

В экономичных алгоритмах обращения теплицевых. матриц (см., напр., [3]) вычисление проводится по рекуррентным формулам и также требует операций. Условие невырожденности главных подматриц может быть ослаблено с сохранением порядка О( п ² )необходимой арифметич. работы.

Иногда операцию О. м. используют с тем, чтобы решать линейные системы по формуле В случае матрицы общего вида такой образ действий имеет мало смысла, т. к. сопровождается проигрышем и в арифметич. работе, и в численной устойчивости по-сравнению с прямым решением линейной системы. Для теплицевых (и родственных им) матриц ситуация иная. Как показывает представление (2), вычисление сводится к выполнению четырех умножений, теплицевых матриц на векторы и вычитанию векторов. Существуют экономичные алгоритмы умножения теплицевой матрицы на вектор, требующие (для порядка п} операций. Для задачи решения теплицевых систем такая асимптотика арифметич. работы пока недостигнута. Поэтому при многократном решении линейных систем с одной и той же теплицевой матрицей и различными правыми частями bпредварительное обращение , по-видимому, целесообразно.

Предварительное О. м. может быть оправданным и в случае многократного решения линейных систем с одной и той же матрицей общего вида на ЭВМ с большим; числом параллельно работающих процессоров. Причина в том, что по сравнению с операцией умножения матрицы на вектор прямые методы решения линейных систем не имеют столь же удобного распараллеливания.

Во многих случаях (напр., в квазиньютоновых методах математич. программирования) требуется обратить матрицу А, отличающуюся от матрицы Вс известной обратной матрицей ранга 1 или (в случае симметричной матрицы В)симметричной матрицей ранга 2. Такая перестройка обратной матрицы может быть выполнена для матриц порядка пза арифметич. операций. Примером может служить следующая формула (см. [4]): если и - векторы-столбцы, то

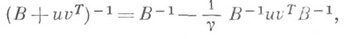
где считается отличным от нуля.

С точки зрения теории вычислительной сложности задача О. м. общего вида имеет (на последовательной машине) сложность того же порядка, что и задача решения линейной системы (при выполнении нек-рых естественных условий на скорость роста сложности обеих задаче увеличением их порядка [5]). Эта сложность имеет порядок, не превышающий n^log₂ ⁷.

Лит.:[1] Воеводин В. В., Численные методы алгебры, М., 1966; [2] Гохберг И. Ц., Фельдман И. А., Уравнения в свертках п проекционные методы их решения, М., 1971; [3] Trench W., "SIAM J. Contr.", 1964, v. 12, p. 512- 522; [4] Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М.- Л., 1963; [5J Ахо А., Хопкрофт Дж., Ульман Дж., Построение и анализ вычислительных алгоритмов, пер. с англ., М., 1979.

С. Д. Икрамов.