- АЭРОДИНАМИКИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ
задачи, связанные с решением основных уравнении аэродинамики, к-рые точно описывают законы движения газообразной среды и ее силового взаимодействия с движущимися в этой среде твердыми телами. Исключение составляет турбулентность, для к-рой не построена сколько-нибудь удовлетворительная математич. модель.
Те процессы, при к-рых турбулентность не возникает или не играет существенной роли, могут быть в принципе достаточно полно исследованы с помощью математпч. решения соответствующих уравнений. Реальные возможности решения отстают от принципиальных, н на основе оценок порядков различных членов в уравнениях создаются упрощенные математич. модели для различных классов аэродинамич. процессов, в к-рых отброшены те или другие "малые" члены из полной системы уравнений аэродинамики. Даже для таких упрощенных моделей возможность получения аналитич. решений ограничена простейшими случаями и в решении практич. задач аэродинамики широко использовались численные методы. С появлением ЭВМ численные методы стали главенствующими.
В соответствии с характером уравнений А. м. з. можно разбить на четыре крупных раздела.
1) Задачи аэродинамики идеальной (невязкой и нетеплопроводной) жидкости. Слово "жидкость" применяется здесь в общем смысле: капельная жидкость и газы.
2) Задачи аэродинамики вязкой жидкости.
3) Задачи аэродинамики излучающего газа.
4) Задачи аэродинамики разреженного газа.
Уравнения идеальной жидкости получаются из общих уравнений при неограниченном возрастании числа Рейнольдса, характеризующего порядок отношения инерционных сил к силам вязкости.
Для большинства прикладных задач аэродинамики самолетов и ракет, гидродинамики корабля числа Рейнольдса весьма велики
 , так что модель идеальной жидкости весьма точно описывает процессы обтекания тел в этих условиях, за исключением области пограничного слоя. Система уравнений аэродинамики идеальной жидкости:
, так что модель идеальной жидкости весьма точно описывает процессы обтекания тел в этих условиях, за исключением области пограничного слоя. Система уравнений аэродинамики идеальной жидкости:

(где
 - вектор скорости,
- вектор скорости,  - плотность,
- плотность, 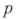 - давление,
- давление,  - ускорение силы тижести,
- ускорение силы тижести,  - внутренняя энергия) является системой уравнений 1-го порядка относительно искомых функций. Это остается в силе и для смесей химически реагирующих газов: к упомянутым уравнениям прибавляются уравнения переноса компонентов смеси и в уравнении энергии добавится выделение тепла вследствие химич. реакций.
- внутренняя энергия) является системой уравнений 1-го порядка относительно искомых функций. Это остается в силе и для смесей химически реагирующих газов: к упомянутым уравнениям прибавляются уравнения переноса компонентов смеси и в уравнении энергии добавится выделение тепла вследствие химич. реакций.
Из модели идеальной жидкости выделяется ряд более упрощенных моделей. Важнейшими являются модель невесомой и модель несжимаемой жидкости. Первая модель - предельный случай общей модели при неограниченном возрастании числа Фруда, характеризующего порядок отношений сил инерции к силам тяжести. Эта модель весьма точна в приложении к аэродинамике самолетов и ракет (число Фруда порядка
 ). Однако для гидродинамики корабля и особенно в метеорологич. применениях аэродинамики сила тяжести играет существенную роль (число Фруда порядка
). Однако для гидродинамики корабля и особенно в метеорологич. применениях аэродинамики сила тяжести играет существенную роль (число Фруда порядка  ).
).
Уравнение несжимаемой жидкости получается из общей системы, если в ней положить плотность
 К этой форме уравнений движения можно придти при стремлении к нулю числа Маха (отношения характерной скорости звука в жидкой среде). В общем случае такое утверждение неверно. Оно справедливо лишь при числах Фруда
К этой форме уравнений движения можно придти при стремлении к нулю числа Маха (отношения характерной скорости звука в жидкой среде). В общем случае такое утверждение неверно. Оно справедливо лишь при числах Фруда  (должно быть
(должно быть  ), а также для процессов, близких к стационарным: число Струхаля (Стро-ухала) - критерии подобия нестационарных движений жидкости или газа - порядка
), а также для процессов, близких к стационарным: число Струхаля (Стро-ухала) - критерии подобия нестационарных движений жидкости или газа - порядка 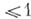
Модель несжимаемой жидкости наиболее проста. Для нее вся система уравнений сводится к одному уравнению Лапласа для потенциала скорости
 Однако только в случае плоскопараллельных движений невесомой жидкости и осесимметричных движений около тел вращения решение аэродинамич. задач сводится к классич. задачам теории непрерывного потенциала. Задача обтекания профиля заданной формы решается классич. методами конформных преобразований. Обтекание тел вращения под нулевым углом атаки определяется классич. решением внешней задачи Неймана для уравнения Лапласа. Ввиду практич. важности этих задач (определение характеристик крыловых профилей, фюзеляжей) были разработаны многочисленные приемы их решения, позволившие относительно простыми вычислениями получить приемлемую точность решения. При использовании ЭВМ эти приемы теряют свой смысл, так как точные численные методы решения указанных задач относятся к простейшим задачам вычислительной математики.
Однако только в случае плоскопараллельных движений невесомой жидкости и осесимметричных движений около тел вращения решение аэродинамич. задач сводится к классич. задачам теории непрерывного потенциала. Задача обтекания профиля заданной формы решается классич. методами конформных преобразований. Обтекание тел вращения под нулевым углом атаки определяется классич. решением внешней задачи Неймана для уравнения Лапласа. Ввиду практич. важности этих задач (определение характеристик крыловых профилей, фюзеляжей) были разработаны многочисленные приемы их решения, позволившие относительно простыми вычислениями получить приемлемую точность решения. При использовании ЭВМ эти приемы теряют свой смысл, так как точные численные методы решения указанных задач относятся к простейшим задачам вычислительной математики.
В пространственном случае формальное решение задачи Неймана для потенциала скоростей лишь в исключительных случаях может соответствовать физически реальной картине обтекания. В вязкой жидкости за телом следует вихревой след. При увеличении числа Рейнольдса этот след утоныпается (при безотрывном обтекании) и в пределе переходит в бесконечно тонкую вихревую поверхность, интенсивность вихревого слоя к-рой лишь в редких случаях обращается в нуль (напр., при плоскопараллельных движениях). Поэтому реальными пространственными задачами несжимаемой жидкости являются задачи с разрывным потенциалом скорости в области течения. Положение этой поверхности разрыва неизвестно, поэтому точная задача обтекания пространственных тел при наличии поверхностей разрыва потенциала в потоке является весьма сложной нелинейной задачей. Лишь в линейном приближении, то есть в предположении, что обтекаемое тело мало возмущает основной равномерный поток (тонкое крыло под малым углом атаки), задача получила решение. В этом случае вихревую поверхность можно считать горизонтальной, условием на ней - постоянство разрыва потенциала вдоль потока. На площади проекции тела заданы нормальные производные от потенциала скорости. В этой постановке были получены аналитич. решения (для круглого и эллиптич. крыла). Для любой же формы крыла разработаны численные методы решения, к-рые делают задачу достаточно простой (см. Крыла теория). В задачах для случая тяжелой жидкости основная трудность состоит в нелинейных граничных условиях для потенциала на свободной поверхности. В точной постановке решены лишь плоские задачи теории волн. Весьма мало продвинута пространственная задача о волнах конечной амплитуды. В то же время в линеаризованной постановке (малые амплитуды волн) задача исследована достаточно полно, и именно линейная теория является основой расчета волнового сопротивления корабля.
Выход летательных аппаратов на большие околозвуковые и сверхзвуковые скорости стимулировал быстрое развитие методов решения задач аэродинамики сжимаемой жидкости. Методы существенно различны в разных диапазонах скоростей: дозвуковые скорости течений, трансзвуковые и сверхзвуковые. В дозвуковом диапазоне уравнения аэродинамики остаются эллиптическими и качественный характер решений сохраняется тем же, что и для несжимаемой жидкости.
В начальный период исследований по аэродинамике сжимаемой жидкости были выполнены многочисленные работы, позволяющие оценивать влияние сжимаемости на аэродинамич. характеристики обтекаемых тел. Все эти методы в том или ином виде использовали линеаризацию относительно скорости невозмущенного потока.
Исключением явился метод Христиановича, который позволял находить точные решения уравнений дозвуковой аэродинамики, но для тела неизвестной заранее формы.
Задачи дозвуковой аэродинамики в практике имеют те же трудности, что и соответствующие задачи для несжимаемой жидкости: решение задач для плоскопараллельных и осесимметричных течений может быть получено численными методами без значительных трудностей ( интегральных соотношений метод, установления метод) . В случае пространственных течений с разрывным потенциалом скоростей решение может быть получено лишь для линеаризированных уравнений. Но эти последние элементарным преобразованием сводятся к уравнениям для несжимаемой жидкости с условиями на границе и на поверхности разрыва, аналогичными несжимаемой жидкости.
Наиболее сложной для математич. решений (в том числе и численных) является область трансзвуковой аэродинамики. Наличие местных сверхзвуковых (гиперболических) зон, заканчивающихся почти всегда ударными волнами, не позволяет вводить к.-л. аналитич. аппроксимации. В то же время эти задачи обладают главным недостатком уравнений эллиптич. типа - распространение влияния любого возмущения на все пространство. Для решения задач трансзвуковой аэродинамики наиболее подходящим является метод установления, заключающийся в том, что решается нестационарная аэро-динамич. задача (исходя из произвольного начального состояния), а решение стационарной задачи обтекания тела трансзвуковым потоком получается как предел решения нестационарной задачи при стремлении времени к бесконечности. Метод этот весьма трудоемкий, но по мере роста эффективности ЭВМ он становится практически вполне осуществимым.
Сверхзвуковая аэродинамика по методам математич. исследований разделяется на три области.
1) Чисто сверхзвуковые течения.
2) Смешанные течения, с образованием локальных дозвуковых зон.
3) Высокотемпературные гиперзвуковые течения, при к-рых в газе возникают химич. реакции.
При более высоких скоростях и, как следствие, температурах возникает ионизация и существенными становятся процессы излучения. Эта часть гиперзвуковой аэродинамики выделяется в специальный раздел, так как математич. задачи, связанные с указанными процессами, резко отличаются от задач "прозрачного" газа.
Задачи чисто сверхзвуковых течений наиболее полно исследованы. Разработанные здесь численные методы характеристик, конечно разностный методы и полухарактеристические позволяют сравнительно просто рассчитывать не только плоскопараллельные или осесимметричные течения, но и пространственные. Исчерпывающе разработана также линейная теория сверхзвуковых течений. Для очень многих практических задач она позволяет получать решения в аналитической форме. Некоторую сложность в этих задачах представляют случаи возникновения слабых ударных волн. Но и эти трудности вычислительного, а не принципиального характера.
В практическом отношении эти задачи ограничиваются обтеканием заостренных тел, а также задачами внутренней аэродинамики (расчет сопел). В то же время при больших сверхзвуковых скоростях не используются заостренные тела (обгорание острых кромок), а у затупления обязательно образуется местная дозвуковая область. После расчета этой области дальнейший расчет течения (уже чисто сверхзвукового) проводится методами сверхзвуковой аэродинамики.
По сравнению с аэродинамикой трансзвуковых течений задачи сверхзвуковой аэродинамики с местными дозвуковыми зонами, хотя таковые являются смешанными, имеют то преимущество, что эти зоны ограничены и не только ограничены, но представляют собой, как правило, узкие зоны в окрестности затупления. Именно это позволило разработать эффективные численные методы для расчета местных дозвуковых зон (метод интегральных соотношений, метод обратных задач, а также метод установления). Следует, однако, отметить, что строгого математич. исследования этих задач пока (1977) не существует. Нет доказательства существования и единственности решения. Поэтому численные методы строятся на основании математич. гипотезы, что условие непрерывности скоростей и ускорений при переходе из дозвуковой в сверхзвуковую область выделяет единственное решение, к-рое и является физически реальным. Все результаты численных расчетов подтверждают эту гипотезу.
Как уже было сказано, после расчета местной дозвуковой зоны (включая сверхзвуковую часть области влияния), дальнейший расчет течения проводится методами чисто сверхзвуковой аэродинамики.
Существует еще круг задач, связанных с гиперзвуковым обтеканием тонких тел (до возникновения химич. реакций). Гиперзвуковые течения возле тонких тел (исключая область затупления), характеризуются малыми изменениями составляющей скорости вдоль основного потока. Этот факт позволяет упростить уравнения так, что задача обтекания тонкого тела заданной формы (в плоском и осесимметричном случаях) становится аналогичной одномерной нестационарной задаче. На этом пути были получены важные качественные характеристики гиперзвуковых течений и установлены приближенные законы подобия, широко используемые также при анализе результатов численных расчетов, позволяя сводить их к весьма компактным зависимостям в широком диапазоне чисел Маха и геометрич. параметров тела.
Аэродинамич. задачи для химически реагирующего газа приводят к необходимости совместного решения уравнений движения и уравнений химич. кинетики. Несмотря на все усложнение системы уравнений, численные методы решения этих задач не отличаются принципиально от задач аэродинамики совершенного газа, приводя лишь к значительному увеличению трудоемкости соответствующих расчетов. Такие расчеты широко внедрены в практику, и поскольку для этого температурного диапазона моделирование натурных условий в аэродинамич. трубах практически неосуществимо, расчетные методы являются основным средством определения аэродинамич. характеристик гиперзвуковых аппаратов.
Теория вязкой жидкости имеет два главных направления - теорию полных уравнений вязкой жидкости (Навье - Стокса уравнения).и пограничного слоя теорию. Уравнения пограничного слоя представляют собой главный член асимптотич. разложения уравнений Навье - Стокса вблизи твердой границы, на к-рой происходит полное или частичное прилипание частиц жидкости к твердой поверхности. Именно это условие нарушает коренным образом решения, соответствующие идеальной жидкости вблизи поверхности обтекаемого тела. Погрешность уравнений пограничного слоя составляет порядок
 т. е. эта теория справедлива при больших числах Рейнольдса (при этом лишь в областях плавного безотрывного обтекания). Несмотря на то, что уравнения пограничного слоя сохраняют все основные члены вязких напряжений, математическая их структура значительно проще. Если полные уравнения являются уравнениями эллиптич. типа, то уравнения пограничного слоя - параболич. типа с характеристиками, направленными по нормали к поверхности, тела.
т. е. эта теория справедлива при больших числах Рейнольдса (при этом лишь в областях плавного безотрывного обтекания). Несмотря на то, что уравнения пограничного слоя сохраняют все основные члены вязких напряжений, математическая их структура значительно проще. Если полные уравнения являются уравнениями эллиптич. типа, то уравнения пограничного слоя - параболич. типа с характеристиками, направленными по нормали к поверхности, тела.
Поэтому они дают возможность "послойного" расчета, т. е. перехода от одного сечения пограничного слоя к другому, независимо от к.-л. условий вне промежутка между этими сечениями.
Важное нрактич. значение теории пограничного слоя (расчет сопротивления, температур поверхности, скорости разрушения поверхности при гиперзвуковых скоростях полета) породило многочисленные приближенные методы его расчета (метод Польхаузена, однопараметрич. метод Кочина - Лойцянского и др.). Однако при применении ЭВМ все эти упрощенные приемы становятся ненужными, так как задача точного численного решения уравнений пограничного слоя, даже в сложных случаях химически реагирующего высокотемпературного газа, не представляет сколько-нибудь большой трудности. Численные схемы могут быть построены таким образом, что на каждом шаге по переменной х(вдоль касательной к контуру тела) система уравнений разбивается на совокупность разделенных дифференциальных уравнений 2-го порядка, что дает весьма большие вычислительные преимущества.
Сказанное относится к плоскопараллельным и осесим-метричным течениям. Трехмерный пограничный слой имеет более сложную структуру. Сами уравнения трехмерного слоя существенно зависят от геометрии обтекаемого тела. Методы решения трехмерного пограничного слоя гораздо меньше разработаны, отчасти потому, что на практике широко используются расчеты по плоским сечениям, хотя и мало обоснованные, но дающие во многих случаях достаточную точность. Для точных уравнений трехмерного слоя нет принципиальных трудностей в решении.
Методы решения полной системы уравнений вязкой жидкости, за исключением немногих частных случаев, когда удавалось получать аналитич. решение, начали развиваться с использованием ЭВМ. Основная трудность в решении этих уравнений состоит в их высоком порядке и неограниченности области влияния. В простейшем случае стационарных движений вязкой несжимаемой жидкости с постоянным коэффициентом вязкости уравнения приводятся к системе двух уравнений 2-го порядка относительно функции тока y и вихря скорости (о. В безразмерной форме их можно записать в виде:
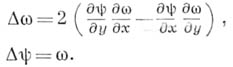
Граничные условия на твердых границах имеются только для функции тока
 Решение этой нелинейной системы 4-го порядка может быть получено лишь с помощью нек-рого итерационного процесса. Итерационный процесс строится таким образом, чтобы на каждом шаге итерации получались раздельные уравнения для вихря и функции тока. Это разделение нужно проводить не только в уравнениях, но и в граничных условиях. Напр., выбирая за первое приближение решение уравнений идеальной жидкости, можно получить следующую систему итераций:
Решение этой нелинейной системы 4-го порядка может быть получено лишь с помощью нек-рого итерационного процесса. Итерационный процесс строится таким образом, чтобы на каждом шаге итерации получались раздельные уравнения для вихря и функции тока. Это разделение нужно проводить не только в уравнениях, но и в граничных условиях. Напр., выбирая за первое приближение решение уравнений идеальной жидкости, можно получить следующую систему итераций:
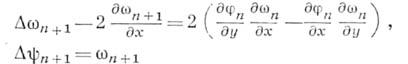
при граничных условиях на твердых границах:

(здесь
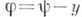 ), т. е. получаем раздельную систему уравнений для вихря и функции тока в
), т. е. получаем раздельную систему уравнений для вихря и функции тока в  -м приближении. Аналогичным образом можно вести решение методом установления, однако для этой цели не обязательно брать реальную систему нестационарных уравнений, а можно рассмотреть более удобную для численных расчетов систему параболич. уравнений:
-м приближении. Аналогичным образом можно вести решение методом установления, однако для этой цели не обязательно брать реальную систему нестационарных уравнений, а можно рассмотреть более удобную для численных расчетов систему параболич. уравнений:

Задача обтекания тел вязкой жидкостью требует не только разработки методов расчета, но и принципиальных исследований. Не ясен вопрос существования стационарного решения при больших числах Рейнольдса (напр., при обтекании цилиндра). Численные методы позволяют найти решение до числа Рейнольдса порядка нескольких сотен, но при больших значениях этого числа численные расчеты не дают сходимости.
В аэродинамике излучающего газа и аэродинамике разряженного газа решены задачи лишь для простейших случаев движения газа. Однако практическая важность этих вопросов привела к появлению - как в том, так и в другом разделе - упрощенных математич. моделей явлений, к-рые часто вообще не являются к.-л. предельными случаями полных уравнений (модель серого излучения, модель диффузного излучения в теории излучающего газа, модель Крука в теории разряженного газа), а лишь качественно отражают зависимости, содержащиеся в полных уравнениях. Решение задач этих разделов не может быть получено малыми объемами вычислений и успешное их разрешение зависит от повышения эффективности ЭВМ.
Лит.. [1] Кочин Н. Е., Ки6ел И. <А., Розе Н. В., Теоретическая гидромеханика, ч. 1-2, М., 1963; [2] Xристианович С. А., Обтекание тел газом при больших дозвуковых скоростях, М., 1940; [3] Седов Л. И., Плоские задачи гидродинамики и аэродинамики, 2 изд., М., 1966; [4] Наyes W., Рrobstein R., Hypersonic flow theory, N. Y. - L., 1959; [5] Черный Г. Г., Течения газа с большой сверхзвуковой скоростью, М., 1959; [6] Белоцерковский О. М., Чушкин П. И., в кн.: Basic developments in fluid dynamics, v. 1, N. Y.-L., 1965; [7] Чушкин П. И., Метод характеристик для пространственных сверхзвуковых течений, М .,1968; [8] Обтекание затупленных тел сверхзвуковым потоком газа, 2 изд., М., 1967; [9] Metody numeryczne w mechanice plynow, Wroclaw, 1969. А. А. Дородницын.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
