НУЛЬМЕРНОЕ ПРОСТРАНСТВО

НУЛЬМЕРНОЕ ПРОСТРАНСТВО

в смысле ind - пространство, обладающее базой из множеств одновременно открытых и замкнутых в нем. Каждое дискретное пространство нульмерно, однако Н. п. может не иметь изолированных точек (пример - пространство рациональных чисел 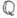). Все нульмерные пространства вполне регулярны. Нульмерность пространства наследуется его подпространствами и влечет сильную несвязность пространства: единственными связными множествами в Н. п. являются одноточечное и пустое. Однако последнее свойство, наз. вполне несвязностью, не равносильно нульмерности. Существуют ненульмерные пространства, в к-рых каждая точка представима в виде пересечения нек-рого семейства открыто-замкнутых множеств, но среди таких пространств нет бикомпактов.

Иногда нульмерность пространства понимается более узко. Пространство наз. нульмерным в смысле dim, если во всякое его конечное открытое покрытие можно вписать открытое покрытие, элементы к-рого не пересекаются. Пространство наз. нульмерным в смысле Ind, если любая окрестность любого его замкнутого подмножества содержит открыто-замкнутую окрестность этого подмножества. В классе -пространств нульмерность в смысле ind вытекает как из нульмерности в смысле dim, так и из нульмерности в смысле Ind. В классе метризуемых пространств со счетной базой, а также в классе бикомпактов указанные три определения нульмерности равносильны. Для всех метризуемых пространств нульмерность в смысле dim равносильна нульмерности в смысле Ind, однако известен пример нульмерного в смысле ind метризуемого пространства, к-рое не нульмерно в смысле Ind. Ни нульмерность в смысле dim, ни нульмерность в смысле Ind не наследуется, вообще говоря, подпространствами. Среди -пространств Н. п. в смысле ind характеризуются с точностью до гомеоморфизма как подпространства обобщенных канторовых дисконтинуумов 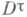- произведений двоеточий. Любые вполне регулярные пространства можно получить как образы Н. п. при достаточно хороших отображениях, напр. при совершенных отображениях и при непрерывных открытых отображениях с бикомпактными прообразами точек. Однако непрерывные отображения, открытые и замкнутые одновременно, сохраняют нульмерность в смысле ind и в смысле Ind. Неизвестно (1981), каждое ли вполне регулярное пространство содержит всюду плотное нульмерное подпространство.

Лит.:[1] Александров П. С, Пасынков Б. А., Введение в теорию размерности..., М., 1973.

А. В. Архангельский.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать реферат

Полезное


Смотреть что такое "НУЛЬМЕРНОЕ ПРОСТРАНСТВО" в других словарях:

  • Нульмерное пространство — в смысле ind ― топологическое пространство, обладающее базой из множеств одновременно открытых и замкнутых в нём. Вариации Иногда нульмерность пространства понимается более узко. Пространство называется нульмерным в смысле dim, если во всякое его …   Википедия

  • Нольмерное пространство — Нульмерное пространство в смысле ind ― топологическое пространство, обладающее базой из множеств одновременно открытых и замкнутых в нём. Вариации Иногда нульмерность пространства понимается более узко. Пространство называется нульмерным в смысле …   Википедия

  • НУЛЬМЕРНОЕ ОТОБРАЖЕНИЕ — непрерывное отображение ( топологич. пространства) такое, что нульмерное множество (в смысле ind) для всякого . Применение Н. о. и близких к ним позволяет свести исследование данного пространства к изучению другого, более простого. Так, многие… …   Математическая энциклопедия

  • БЭРА ПРОСТРАНСТВО — 1) Всякое пространство, в к ром верна Бэра теорема (о полных пространствах). 2) Метрич. пространство, точками к рого являются конечные последовательности натуральных чисел, .а расстояние задается формулой: где первое натуральное k, для к рого Это …   Математическая энциклопедия

  • Трёхмерное пространство — Трёхмерная метрика пространства …   Википедия

  • ТОПОЛОГИЧЕСКОЕ ПРОИЗВЕДЕНИЕ — тихоновскоe произведение, семейства топологических пространств топологич. пространство где X декартово произведение (т. е. полное прямое произведение) множеств по и слабейшая (т. е. наименьшая) топология на множестве Xтакая, что все отображения… …   Математическая энциклопедия

  • Размерность Лебега — У этого термина существуют и другие значения, см. Размерность (значения). Размерность Лебега или топологическая размерность размерность, определенная посредством покрытий, важнейший инвариант топологического пространства. Размерность Лебега… …   Википедия

  • Размерность топологического пространства — Размерность Лебега или топологическая размерность размерность, определенная посредством покрытий, важнейший инвариант топологического пространства. Размерность Лебега пространства X обычно обозначается . Содержание 1 Определение 1.1 Для… …   Википедия

  • КАНТОРОВО МНОЖЕСТВО — подмножество отрезка [0, 1] числовой оси, состоящее из всех чисел вида где ei равно 0 или 2. Построено Г. Кантором (G. Cantor, 1883). Геометрич. его описание (см. рис.): из отрезка [0, 1] выбрасывается его средняя треть интервал , затем из… …   Математическая энциклопедия

  • БИКОМПАКТНОЕ РАСШИРЕНИЕ — (би)компактификация, расширение топологического пространства, являющееся бикомпактным пространством. Б. р. существуют у любого топологич. пространства, у любого T1 пространства есть Б. р., являющиеся T1 пространствами, но наибольший интерес… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»