- КАНТОРОВО МНОЖЕСТВО
- подмножество отрезка [0, 1] числовой оси, состоящее из всех чисел вида
где ei равно 0 или 2. Построено Г. Кантором (G. Cantor, 1883). Геометрич. его описание (см. рис.): из отрезка [0, 1] выбрасывается его средняя треть - интервал 
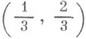, затем из оставшихся отрезков 
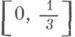и 
выбрасываются интервалы 
и из оставшихся четырех отрезков также выбрасываются 
их средние трети, и т. д.; то, что останется после выбрасывания всех этих интервалов (смежных интервалов), суммарная длина к-рых равна 1, и есть канторово совершенное множество (Кантора множество; канторов дисконтинуум); оно нигде не плотно на числовой прямой, имеет мощность континуума.
С топологич. точки зрения К. м.- нульмерный совершенный (т. е. без изолированных точек), компакт, причем с точностью до гомеоморфизма существует единственный такой компакт. Все ограниченные совершенные нигде не плотные множества на числовой прямой суть подобные множества. К. м. гомеоморфно счетной степени
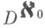простого двоеточия Dи является пространством топологич. группы 
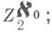К. м. универсально в двух смыслах: во-первых, всякое нульмерное пространство со счетной базой гомеоморфно подмножеству К. м.; 2) во-вторых, всякий компакт является непрерывным образом К. м. (теорема Александрова). Эта теорема кладет начало теории диадических бикомпактов и показывает, что многие компакты похожи друг на друга с функциональной точки зрения. Так, в частности, все совершенные компакты имеют одинаковые булевы алгебры всех канонич. открытых множеств. Существование специальных отображений К. м. на компакты позволяет доказать, что банаховы алгебры всех непрерывных функций на двух произвольных совершенных компактах (напр., на отрезке и квадрате) линейно гомеоморфны. Далее, К. м. и возможность отобразить его на произвольный компакт лежат в основе построения многих примеров, интересных с точки зрения топологии и теории функций. Одним из них является так наз. канторова лестница- график непрерывного монотонного отображения отрезка [0, 1] на себя, производная к-рого определена и равна нулю на множестве меры 1. Хотя стандартное К. м. имеет меру нуль, существуют нигде не плотные на отрезке совершенные компакты меры, сколь угодно близкой к единице.Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977.
В. В. Федорчук.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
