- ТОПОЛОГИЧЕСКОЕ ПРОИЗВЕДЕНИЕ
тихоновскоe произведение, семейства топологических пространств
 - топологич. пространство
- топологич. пространство  где X - декартово произведение (т. е. полное прямое произведение) множеств
где X - декартово произведение (т. е. полное прямое произведение) множеств  по
по 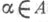 и
и  - слабейшая (т. е. наименьшая) топология на множестве Xтакая, что все отображения естественного проектирования
- слабейшая (т. е. наименьшая) топология на множестве Xтакая, что все отображения естественного проектирования  непрерывны. Топология
непрерывны. Топология  наз. при этом топологией произведения, а Т. п.
наз. при этом топологией произведения, а Т. п.  наз. также топологич. произведением семейства пространств
наз. также топологич. произведением семейства пространств 
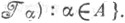
Стандартной базой тоиологич. пространства служит семейство всех множеств вида
служит семейство всех множеств вида 
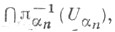 где
где  - произвольный конечный набор элементов индексирующего множества А, а
- произвольный конечный набор элементов индексирующего множества А, а  - любой элемент топологии
- любой элемент топологии  i=l, . . ., п.
i=l, . . ., п.
Вчастности, если семейство состоит из двух пространств Xи Y, то базу топологии произведения
состоит из двух пространств Xи Y, то базу топологии произведения  образуют множества вида
образуют множества вида  гдо U - произвольное открытое множество в X, а V- произвольное открытое множество в Y. Аналогично описывается база топологии произведения любого конечного упорядоченного множества топологич. пространств. Примеры Т. п.: плоскость - произведение двух прямых, n-мерное пространство
гдо U - произвольное открытое множество в X, а V- произвольное открытое множество в Y. Аналогично описывается база топологии произведения любого конечного упорядоченного множества топологич. пространств. Примеры Т. п.: плоскость - произведение двух прямых, n-мерное пространство  - произведение ппрямых, тор - произведение двух окружностей.
- произведение ппрямых, тор - произведение двух окружностей.
Первоначальные попытки определения Т. п. бесконечного множества топологич. пространств относились к случаю метризуемых сомножителей. Соответственно, топологию произведения пытались указать в терминах сходимости обычных (счетных) последовательностей. Когда семейство сомножителей несчетно, получить на этом пути тот же результат, что и выше, было невозможно, так как оператор замыкания в Т. п. несчетного множества неодноточечных метризуемых пространств не может быть описан на языке сходящихся последовательностей или сведен к замыканиям счетных множеств.
Определение Т. п. произвольного бесконечного множества тоиологич. пространств было дано А. Н. Тихоновым (1925). Он же доказал, что Т. п. бикомпактных пространств всегда является бикомпактным пространством.
Операция Т. п. является одним из главных средств формирования новых топологич. объектов из уже имею щихся. С ее помощью конструируется ряд основных стандартных объектов общей топологии - в частности, тихоновские кубы определяемые как топологич. произведение семейства мощности
определяемые как топологич. произведение семейства мощности 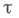 отрезков числовой прямой. По теореме Тихонова, все тихоновские кубы бикомпактны. А. Н. Тихонов доказал, что всякое вполне регулярное T1 -пространство гомeоморфно подпространству нек-рого куба
отрезков числовой прямой. По теореме Тихонова, все тихоновские кубы бикомпактны. А. Н. Тихонов доказал, что всякое вполне регулярное T1 -пространство гомeоморфно подпространству нек-рого куба 
Кроме кубов важную роль в топологии играют пространства
важную роль в топологии играют пространства  и
и  являющиеся соответственно произведениями
являющиеся соответственно произведениями 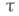 штук пространств, состоящих из двух изолированных точек (простых двоеточий D)и двухточечных пространств с одной изолированной точкой (связных двоеточий F). Всякий компакт есть непрерывный образ канторова совершенного множества, т. е. пространства, гомеоморфного произведению счетного числа простых двоеточий D; всякое индуктивно нульмерное пространство, т. е. T0 -пространство, в к-ром открыто-замкнутые множества образуют базу, гомеоморфно подмножеству нек-рого канторова дисконтинуума
штук пространств, состоящих из двух изолированных точек (простых двоеточий D)и двухточечных пространств с одной изолированной точкой (связных двоеточий F). Всякий компакт есть непрерывный образ канторова совершенного множества, т. е. пространства, гомеоморфного произведению счетного числа простых двоеточий D; всякое индуктивно нульмерное пространство, т. е. T0 -пространство, в к-ром открыто-замкнутые множества образуют базу, гомеоморфно подмножеству нек-рого канторова дисконтинуума  всякое T0 -пространство гомеоморфно подмножеству пространства
всякое T0 -пространство гомеоморфно подмножеству пространства 
В связи с силой и ролью операции Т. п. центральное место в проблематике общей топологии занимают вопросы поведения топологич. свойств при операции Т. н. Устойчивы относительно операции Т. п. классы хаусдорфовых пространств, регулярных пространств и вполне регулярных пространств. Но произведение нормального пространства на отрезок может быть не нормальным пространством, не устойчивым относительно операции Т. п., даже в случае конечного числа сомножителей, такие важные топологич. свойства, как линделёфовость и паракомпактность.
Важную роль в общей топологии и ее приложениях (в частности, к построению моделей теории множеств) играет теорема: число Суслина Т. п. любого множества сепарабельных топологич. пространств счетно. В частности, счетно число Суслина любого тихоновского куба.
Операция Т. п. порождает, путем выделения во всем Т. п. определенных подпространств, весьма полезные операции -произведения и
-произведения и  -произведения. К совершенно иной топологии на декартовом произведении множеств
-произведения. К совершенно иной топологии на декартовом произведении множеств  приводит операция ящичного произведения топологий
приводит операция ящичного произведения топологий 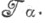
Лит.:[1] Архангельский А. В., IIономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974; [2] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; [3] Александров П. С., Введение в теорию множеств и общую топологию, М., 1977.
А. В. Архангельский, В. В. Федорчук.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
