НЕОРИЕНТИРУЕМОЕ МНОГООБРАЗИЕ
- НЕОРИЕНТИРУЕМОЕ МНОГООБРАЗИЕ
- многообразие, не допускающее ориентации. Таковы, напр., Мёбиуса лист, Клейна поверхность, проективное пространство 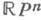 четной размерности, М. И. Войцеховский. НЕОСОБАЯ ГРАНИЧНАЯ ТОЧКА, правильная граничная точк а,- достижимая граничная точка
четной размерности, М. И. Войцеховский. НЕОСОБАЯ ГРАНИЧНАЯ ТОЧКА, правильная граничная точк а,- достижимая граничная точка  области определения Dоднозначной аналитич. ции
области определения Dоднозначной аналитич. ции 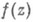 комплексного переменного z такая, что
комплексного переменного z такая, что  аналитически продолжается в
аналитически продолжается в  вдоль любого пути, ведущего из
вдоль любого пути, ведущего из  в
в  . Иначе говоря, Н. г. т.- это достижимая граничная точка, не являющаяся особой граничной точкой. См. также Особая точка аналитической функции.
. Иначе говоря, Н. г. т.- это достижимая граничная точка, не являющаяся особой граничной точкой. См. также Особая точка аналитической функции.
Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "НЕОРИЕНТИРУЕМОЕ МНОГООБРАЗИЕ" в других словарях:
ДВУМЕРНОЕ МНОГООБРАЗИЕ — топологическое пространство, каждая точка к рого обладает окрестностью, гомеоморфной плоскости или полуплоскости. Д. м. наиболее наглядный класс многообразий: к ним относятся сфера, круг, лист Мёбиуса, проективная плоскость, бутылка Клейна и др.… … Математическая энциклопедия
Фундаментальный класс — Фундаментальным классом называется гомологический класс ориентированного многообразия, который соответствует «целому многообразию». Интуитивно фундаментальный класс можно себе представить как сумму симплексов максимальной размерности подходящей… … Википедия
ПРОЕКТИВНАЯ ПЛОСКОСТЬ — двумерное проективное пространство, инцидентностная структура , где элементы множества наз. точкам и, элементы множества прямыми, а I отношение инцидентности. Инцидентностная структура удовлетворяет следующим аксиомам: 1) для любых двух различных … Математическая энциклопедия
СФЕРИЧЕСКОЕ ОТОБРАЖЕНИЕ — отображение гладкой ориентируемой (гипер)поверхности Mk пространства Ek+l в (единичную) сферу Sk с центром в начале координат Ek+l, сопоставляющее точке точку с радиус вектором (единичной) нормалью к Mk в х. Иначе, С. о. определяется поливектором … Математическая энциклопедия
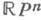 четной размерности, М. И. Войцеховский. НЕОСОБАЯ ГРАНИЧНАЯ ТОЧКА, правильная граничная точк а,- достижимая граничная точка
четной размерности, М. И. Войцеховский. НЕОСОБАЯ ГРАНИЧНАЯ ТОЧКА, правильная граничная точк а,- достижимая граничная точка  области определения Dоднозначной аналитич. ции
области определения Dоднозначной аналитич. ции 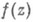 комплексного переменного z такая, что
комплексного переменного z такая, что  аналитически продолжается в
аналитически продолжается в  вдоль любого пути, ведущего из
вдоль любого пути, ведущего из  в
в  . Иначе говоря, Н. г. т.- это достижимая граничная точка, не являющаяся особой граничной точкой. См. также Особая точка аналитической функции.
. Иначе говоря, Н. г. т.- это достижимая граничная точка, не являющаяся особой граничной точкой. См. также Особая точка аналитической функции.